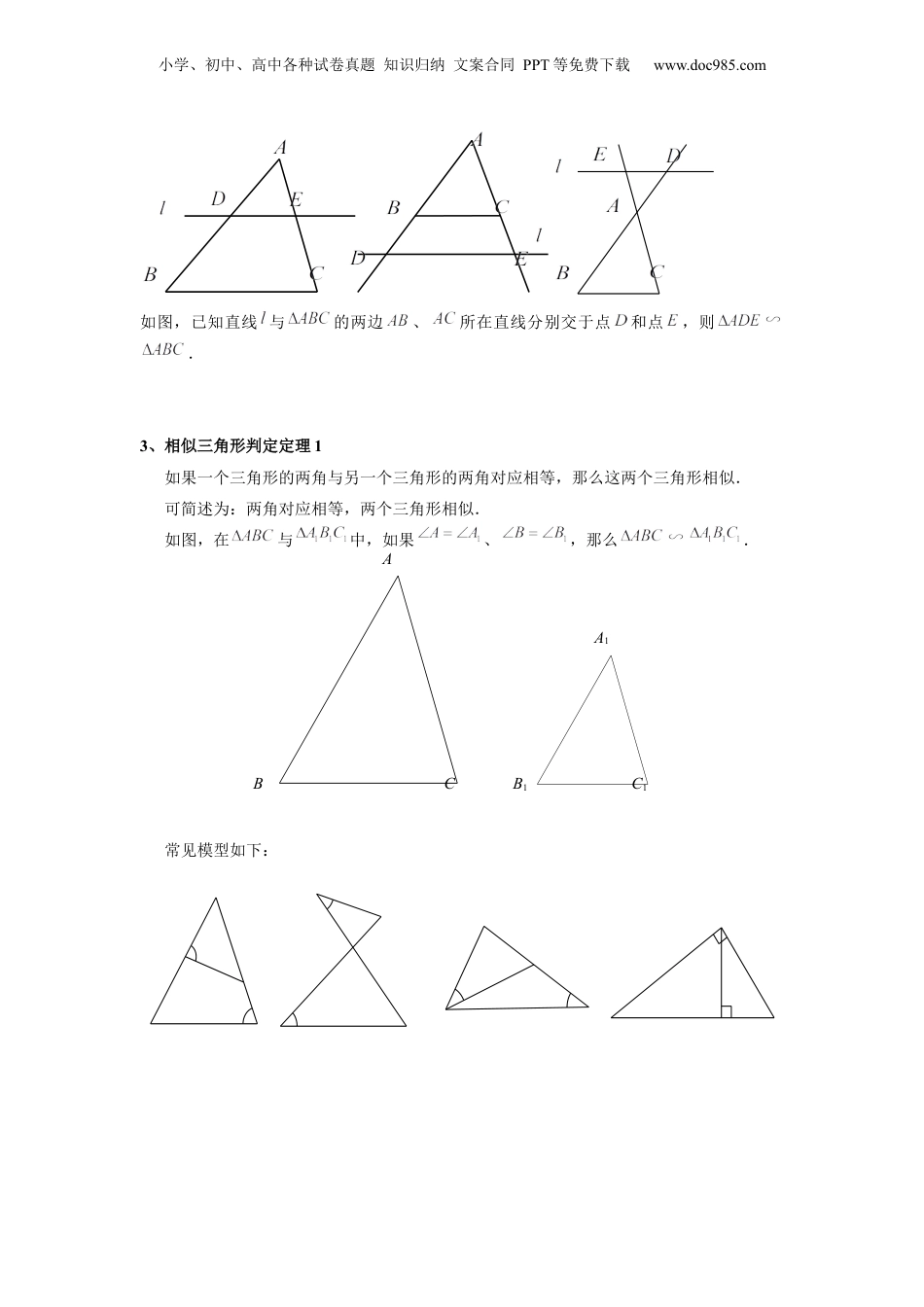
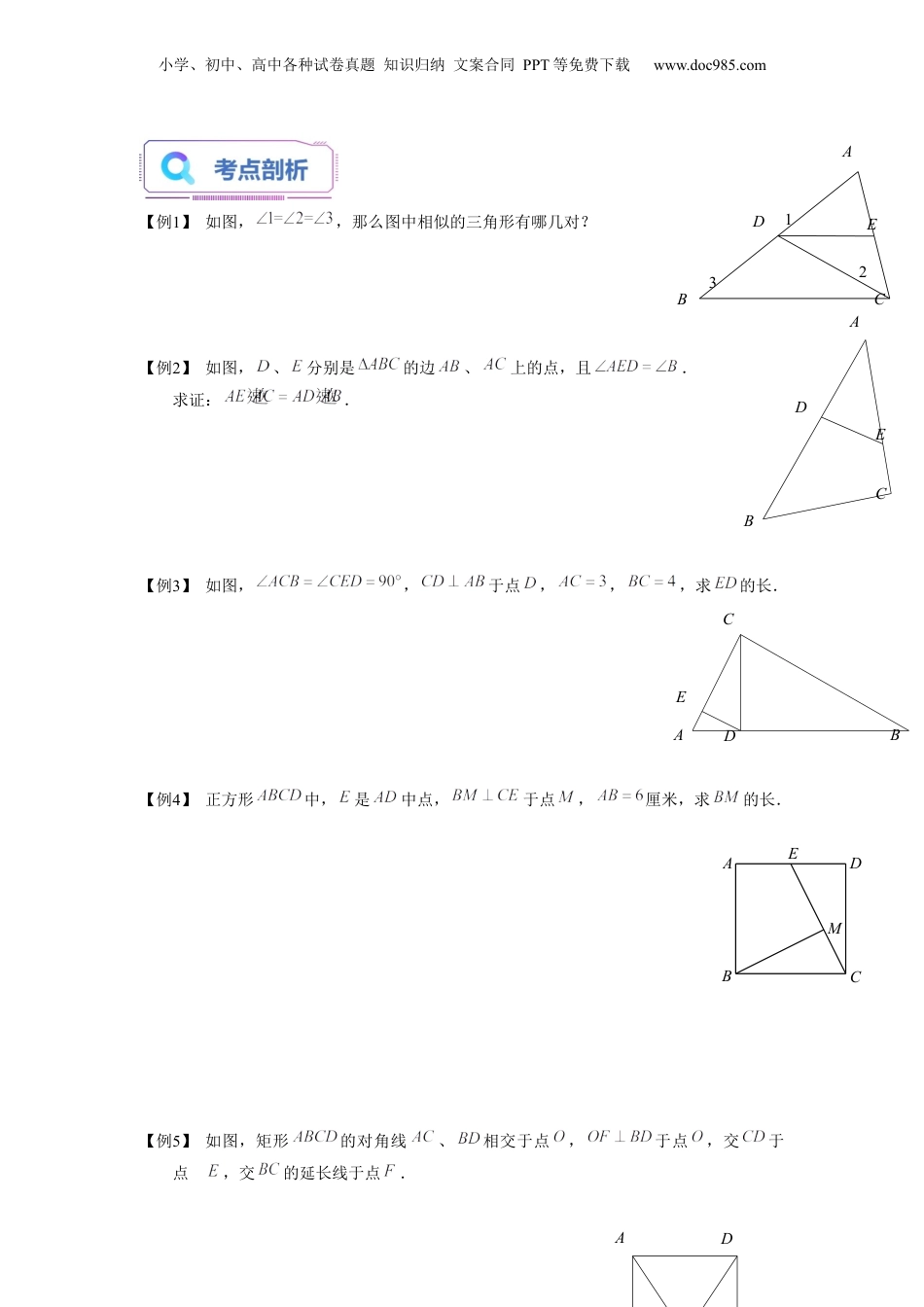
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第04讲相似三角形的判定（一）掌握相似三角形的定义掌握相似三角形判定定理1和相似三角形判定定理2重点是根据已知条件灵活运用这两种判定定理，以及这两者之间的相互结合．模块一：相似三角形判定定理11、相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等，且它们各有的三边对应成比例，那么这两个三角形叫做相似三角形．如图，是的中位线，那么在与中，，，；．由相似三角形的定义，可知这两个三角形相似．用符号来表示，记作，其中点与点、点与点、点与点分别是对应顶点；符号“”读作“相似于”．用符号表示两个相似三角形时，通常把对应顶点的字母分别写在三角形记号“”后相应的位置上．根据相似三角形的定义，可以得出：（1）相似三角形的对应角相等，对应边成比例；两个相似三角形的对应边的比，叫做这两个三角形的相似比（或相似系数）．（2）如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似．2、相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似．ECBAD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com如图，已知直线与的两边、所在直线分别交于点和点，则．3、相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似．可简述为：两角对应相等，两个三角形相似．如图，在与中，如果、，那么．常见模型如下：C1B1A1CBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comEMDCBA【例1】如图，，那么图中相似的三角形有哪几对？【例2】如图，、分别是的边、上的点，且．求证：．【例3】如图，，于点，，，求的长．【例4】正方形中，是中点，于点，厘米，求的长．【例5】如图，矩形的对角线、相交于点，于点，交于点，交的延长线于点．EDCBADA321EDCBAEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com求证：．模块二：相似三角形判定定理21、相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．可简述为：两边对应成比例且夹角相等，两个三角形相似．如图，在与中，，，那么．【例6】如图，在与C1B1A1CBAA1A小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com中，，，求证：．【例7】如图，四边形的对角线与相交于点，，，，．求证：与是相似三角形．【例8】已知，在中，、是的两条高，、交于点．求证：（1）；（2）．【例9】如图，点是的垂心（垂心即三角形三条高所在直线的交点），联结交的延长线于点，联结交的延长线于点，联结．求证：．ODCBAEDCBAGFECBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例10】如图，在中，，是边上的高，点在线段上，，，垂足分别为、．求证：（1）；（2）．一、单选题1.（2022秋·上海徐汇·九年级上海市田林第三中学校考期中）下列两个图形一定相似的是（）A．两个等腰三角形；B．两个等边三角形；C．两个矩形；D．两个梯形．2.（2023·上海·一模）如图，已知与，下列条件一定能推得它们相似的是（）A．B．C．D．GFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3.（2022秋·上海嘉定·九年级校考期中）下列各组条件中，一定能推得与相似的是（）A．且B．且C．且D．且4.（2022秋·上海·九年级校考期中）依据下列条件不能判定和相似的是（）A．，，B．，，，，，C．，，，，，D．，，，，5.（2023·上海·一模）下列说法中，正确的是（）A．两个矩形必相似B．两个含角的等腰三角形必相似C．两个菱形必相似D．两个含角的直角三角形必相似6.（2022秋·上海静安·九年级上海市华东模范中学校考期中）下列五幅图均是由边长为1的16个小正方形组成的正方形网格，网格中的三角形的顶点都在小正方形的顶点上，那么在下列右边四幅图中的三角形，与左图中的△ABC相似的个数有（）A．1个B．2个C．3个D．4个7....