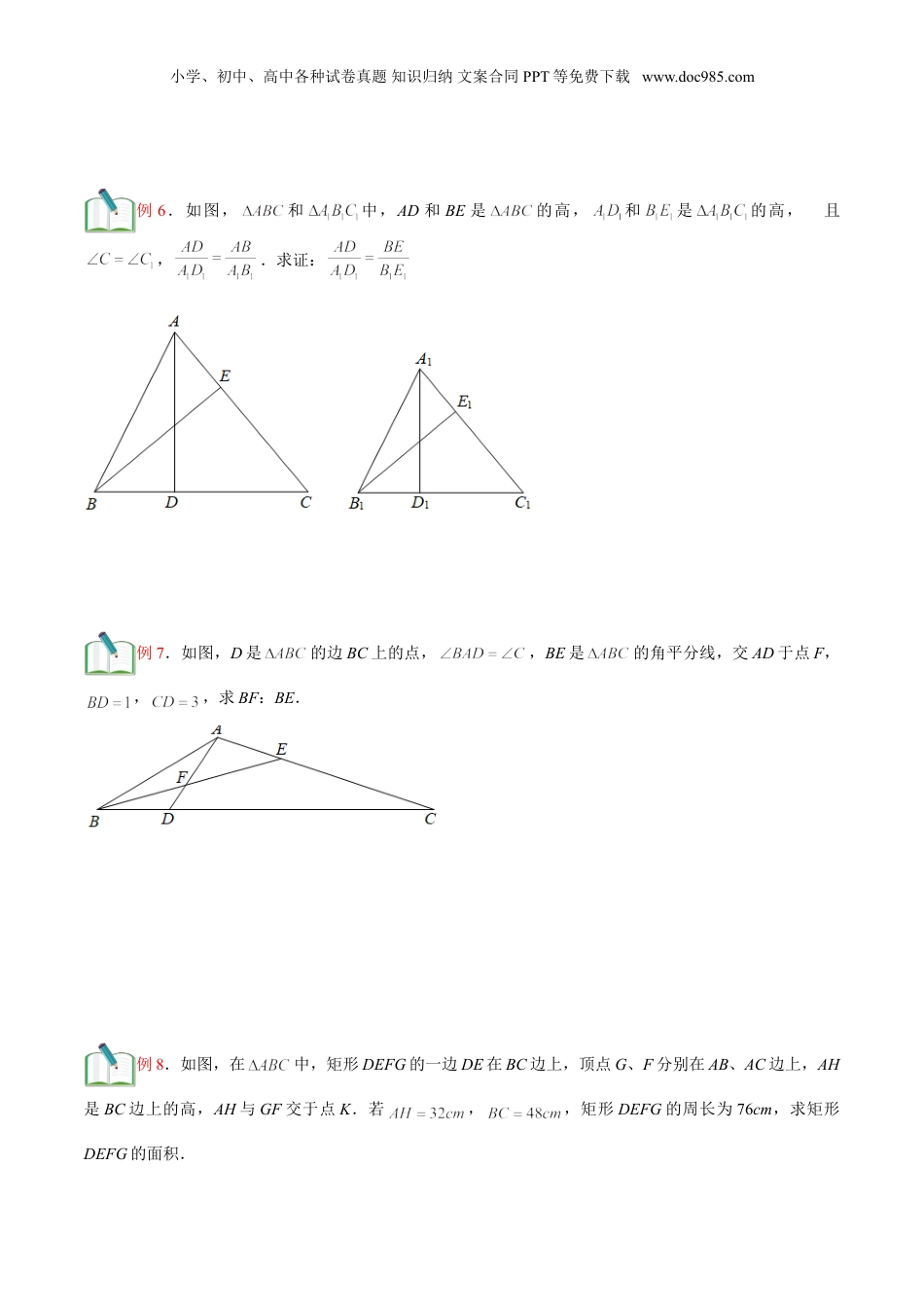
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第6讲相似三角形的性质【学习目标】相似三角形的性质是九年级数学上学期第一章第三节的内容，本讲主要讲解相似三角形的3个性质定理．重点是灵活应用相似三角形的性质，难点是相似三角形的性质与判定的互相结合．【基础知识】一：相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比．二：相似三角形性质定理2相似三角形周长的比等于相似比．三：相似三角形性质定理3相似三角形的面积的比等于相似比的平方．【考点剖析】考点一：一：相似三角形性质定理1例1．已知∽，顶点A、B、C分别与A1、B1、C1对应，，BE、B1E1分别是它们的对应中线，且．求B1E1的长．例2．已知∽，顶点A、B、C分别与A1、B1、C1对应，，,的平分线A1D1的长为6，求的平分线的长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例3．求证：相似三角形对应高的比等于相似比．例4．求证：相似三角形对应中线的比等于相似比．例5．求证：相似三角形对应角平分线的比等于相似比．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例6．如图，和中，AD和BE是的高，和是的高，且，．求证：例7．如图，D是的边BC上的点，，BE是的角平分线，交AD于点F，，，求BF：BE．例8．如图，在中，矩形DEFG的一边DE在BC边上，顶点G、F分别在AB、AC边上，AH是BC边上的高，AH与GF交于点K．若，，矩形DEFG的周长为76cm，求矩形DEFG的面积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点二：相似三角形性质定理2例1．若∽，与的相似比为1:2，则与的周长比为()（A）1:4（B）1:2（C）2:1（D）例2．∽，它们的对应的中线比为2:3，则它们的周长比是．例3．已知∽，顶点A、B、C分别与A1、B1、C1对应，它们的周长分别为48和60，且，，求BC和A1B1的长．例4．如果两个相似三角形的最长边分别为35厘米和14厘米，它们的周长相差60厘米，那么大三角形的周长是．例5．如图，在中，，，，AD是BC边上的高．将沿EF折叠，使点A与点D重合，则的周长为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例6．如图，梯形ABCD的周长为16厘米，上底厘米，下底厘米，分别延长AD和BC交于点P，求的周长．例7．如图，在中，，，，点P在AC上（与点A、C不重合），点Q在BC上，PQ//AB．当的周长与四边形PABQ的周长相等时，求CP的长．考点三：相似三角形性质定理3例1．（1）如果把一个三角形的三边的长扩大为原来的100倍，那么这个三角形的面积扩大为原来的倍；（2）如果一个三角形保持形状不变但面积扩大为原来的100倍，那么这个三角形的边长扩大为原来的倍．例2．两个相似三角形的面积分别为5cm2和16cm2，则它们的对应角的平分线的比为（）（A）（B）（C）（D）以上都不对．例3．如图，点D、E分别在的边AB和AC上，DE//BC，，，．求小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com的值．例4．如图，在中，D是AB上一点，若，，，，求的面积．例5．如图，在中，点D、E在AB、AC上，DE//BC，和四边形BCED的面积相等，求AD:BD的值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例6．如图，在正三角形ABC中，D、E、F分别是BC、AC、AB上的点，，，，则的面积与的面积之比等于（）（A）1:3（B）2:3（C）（D）例7．如图，在中，，，D、E分别为垂足．若，，求四边形DEAB的面积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例8．如图，在矩形ABCD中，AB=2cm，BC=4cm，对角线AC与BD交于点O，点E在BC边上，DE于AC交于点F，．求：（1）BE的长；（2）的面积．例9．如图，中，点D是BC延长线上一点，直线EF//BD交AB于点E，交AC于点G，交AD于点F，若，求的值．【过关检测】一、单选题1．（2021·上海九年级一模）在梯形中，，对角线与相交于点O，下列说法中，错误的是（）A．B．C．D．2．（2020·上海市曹杨二中附属江桥实验中学九年级期中）已知两个相似三角形的相似比...