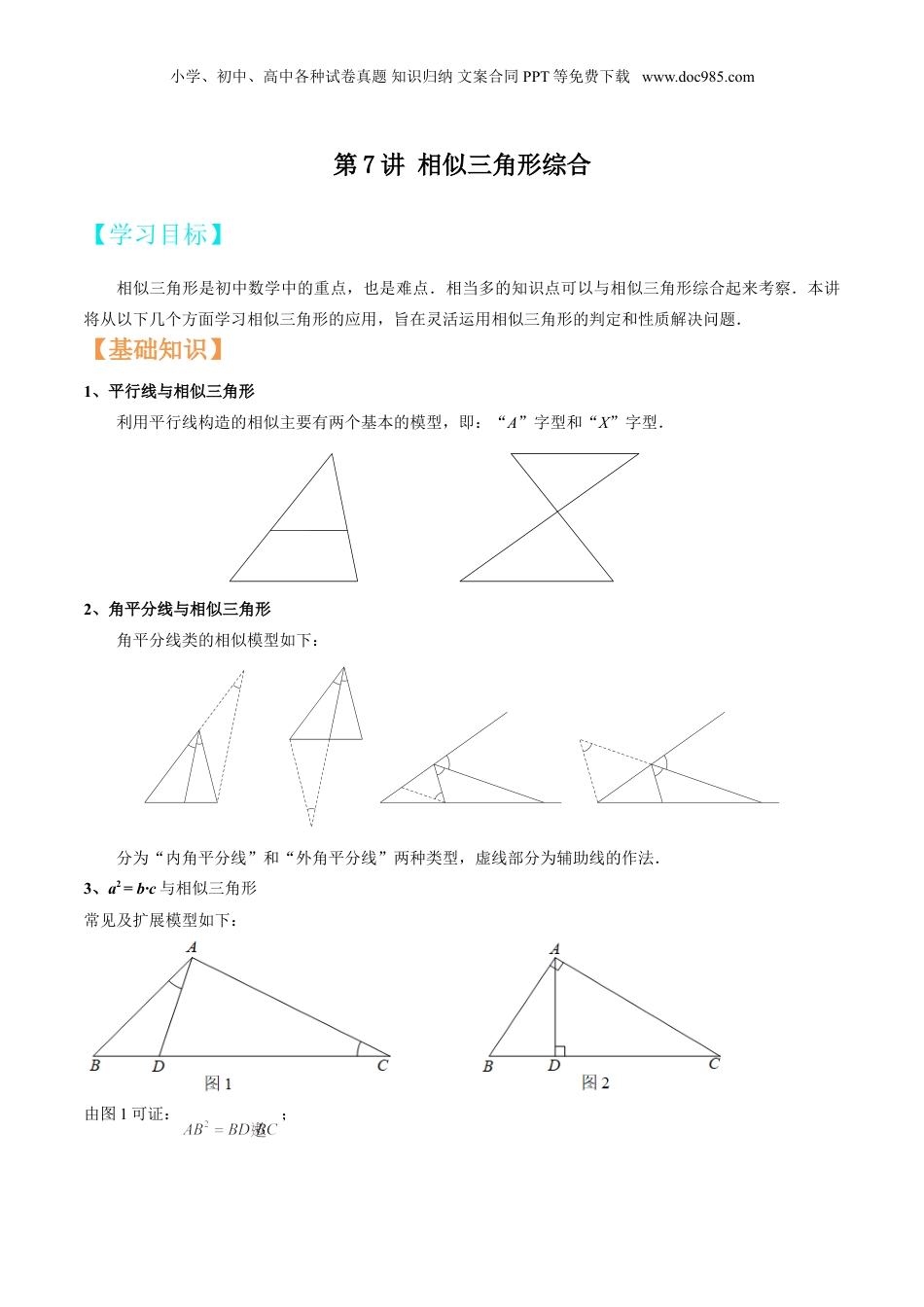
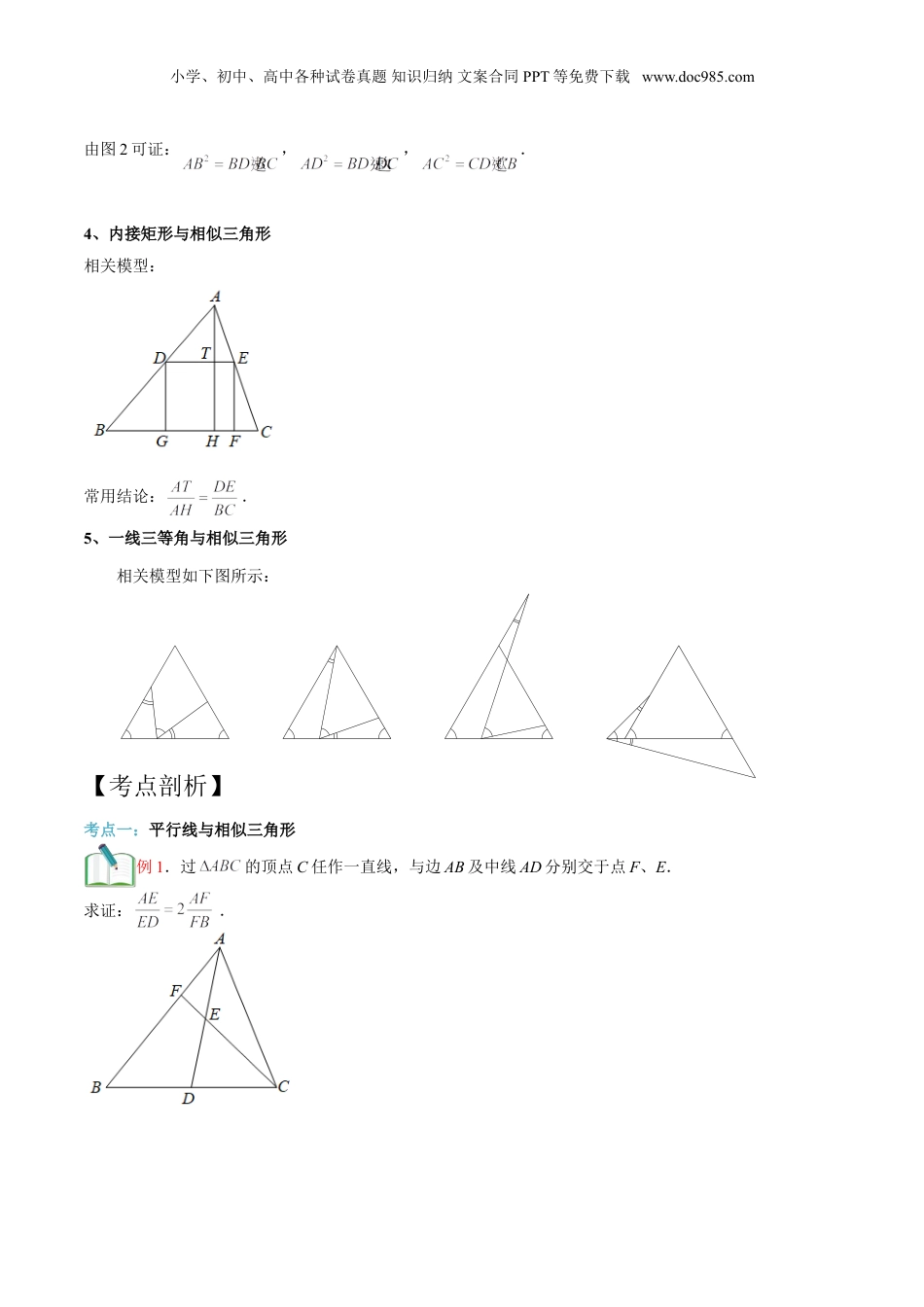
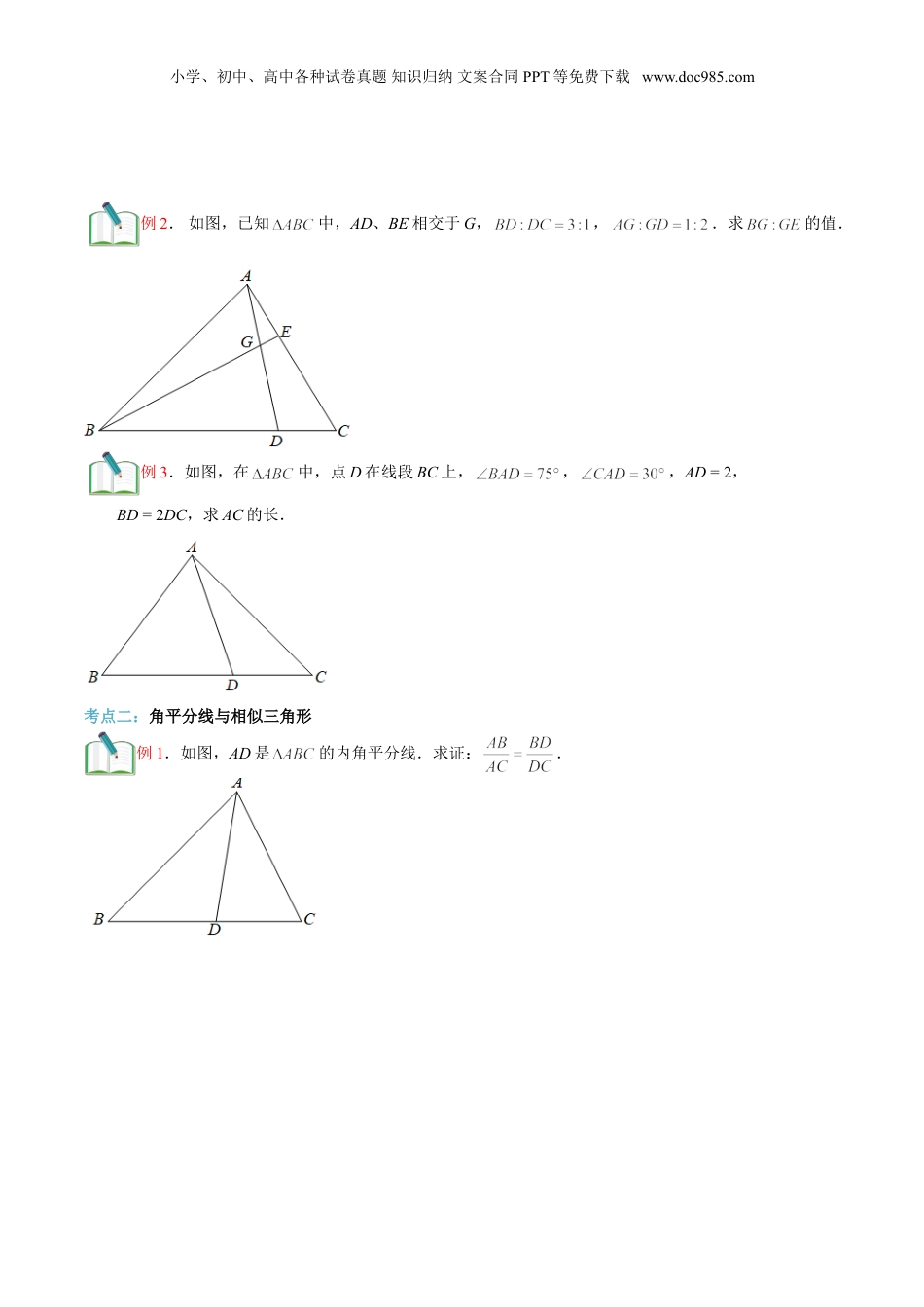
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第7讲相似三角形综合【学习目标】相似三角形是初中数学中的重点，也是难点．相当多的知识点可以与相似三角形综合起来考察．本讲将从以下几个方面学习相似三角形的应用，旨在灵活运用相似三角形的判定和性质解决问题．【基础知识】1、平行线与相似三角形利用平行线构造的相似主要有两个基本的模型，即：“A”字型和“X”字型．2、角平分线与相似三角形角平分线类的相似模型如下：分为“内角平分线”和“外角平分线”两种类型，虚线部分为辅助线的作法．3、a2=b·c与相似三角形常见及扩展模型如下：由图1可证：；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com由图2可证：，，．4、内接矩形与相似三角形相关模型：常用结论：．5、一线三等角与相似三角形相关模型如下图所示：【考点剖析】考点一：平行线与相似三角形例1．过的顶点C任作一直线，与边AB及中线AD分别交于点F、E．求证：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例2．如图，已知中，AD、BE相交于G，，．求的值．例3．如图，在中，点D在线段BC上，，，AD=2，BD=2DC，求AC的长．考点二：角平分线与相似三角形例1．如图，AD是的内角平分线．求证：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例2．如图，在中，，过点C作CE//AB，交的平分线AD于E．（1）不添加字母，找出图中所有的相似三角形，并证明；（2）求证：．考点三：a2=b·c与相似三角形例1．如图，中，，于点D．求证：．例2．如图，已知等腰三角形ABC中，AB=AC，高AD，BE相交于点H．求证：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例3．如图，在直角梯形ABCD中，AB//CD，ABBC，对角线ACBD，垂足为E，AD=BD，过E的直线EF//AB交AD于点F．（1）AF=BE；（2）AF2=AE·EC．考点四：内接矩形与相似三角形例1．如图，中，，，，四边形DEFG为正方形，其中D、E在边AC、BC上，F、G在AB上，求正方形DEFG的边长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点五：一线三等角与相似三角形例1．已知，在等腰中，AB=AC=10，以BC的中点D为顶点作，分别交AB、AC于点E、F，AE=6，AF=4，求底边BC的长．考点六：旋转与相似三角形例1．如图，直角梯形ABCD中，，AD//BC，BC=CD，E为梯形内一点，且，将绕点C旋转90°使BC与DC重合，得到，联结EF交CD于M．已知BC=5，CF=3，则DM:MC的值为（）A．B．C．D．考点七：函数与相似三角形例1．如图，已知与都是等边三角形，点D在BC边上（点D不与B、C重合），DE与AC相交于点F．（1）求证：∽；（2）若BC=1，设BD=x，CF=y，求y关于x的函数解析式及定义域；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（3）当x为何值时，？【过关检测】一、单选题1．（2019·上海）如图，路灯距地面8米，身高1.6米的小明从距离灯的底部（点O）20米的点A处，沿OA所在的直线行走14米到点B时，人影的长度()A．增大1.5米B．减小1.5米C．增大3.5米D．减小3.5米2．（2019·上海）如图，梯形ABCD中，ABCD∥，∠A=90°，E在AD上，且CE平分∠BCD，BE平分∠ABC，则下列关系式中成立的有()①；②；③；④CE2=CD×BC；⑤BE2=AE×BC小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．2个B．3个C．4个D．5个二、填空题3．（2019·上海民办桃李园实验学校）在中，，G是的重心，过G作边BC的平行线交AC于点H，则GH的长为_________.4．（2019·上海）如图，M是▭ABCD的AB的中点，CM交BD于E，则图中阴影部分的面积与▱ABCD的面积之比为_____．5．（2019·上海市民办新北郊初级中学九年级期中）如图，在中，点、分别在、上，且，若，，那么______．6．（2021·上海九年级专题练习）在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF．如果△DEF与小学、初中、高中各种试卷真题知识归纳文案合...