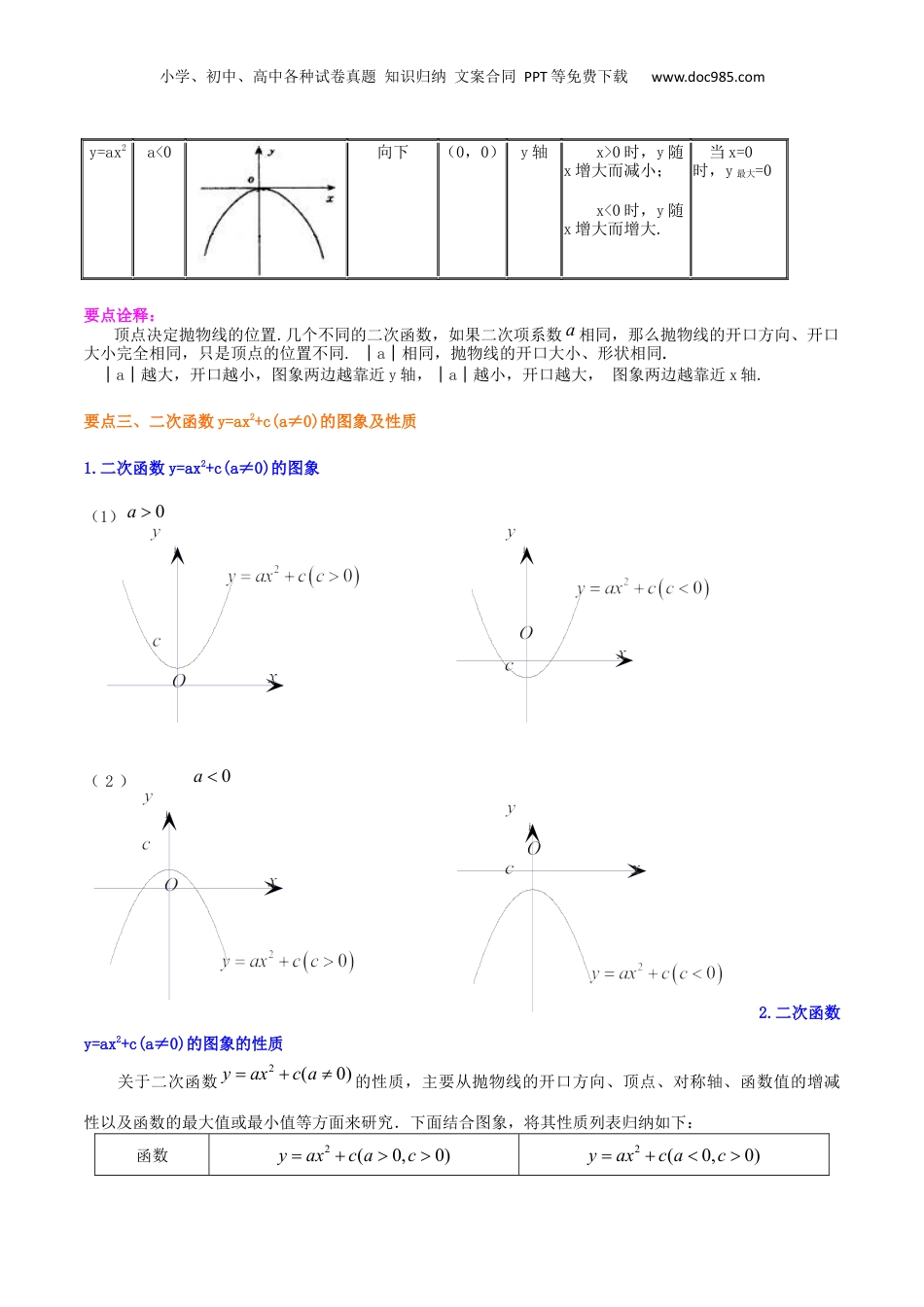
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题16二次函数y=ax^2与y=ax^2+c图像与性质（基础）【目标导向】1．理解二次函数的概念，能用待定系数法确定二次函数的解析式；2．会用描点法画出二次函数y=ax2(a≠0)与20yaxca的图象，并结合图象理解抛物线、对称轴、顶点、开口方向等概念；3.掌握二次函数y=ax2(a≠0)与20yaxca的图象的性质，掌握二次函数20yaxa与20yaxca之间的关系；（上加下减）。【知识要点精讲梳理】要点一、二次函数的概念1.二次函数的概念一般地，形如y=ax2+bx+c（a≠0，a,b,c为常数）的函数是二次函数.若b=0，则y=ax2+c；若c=0，则y=ax2+bx；若b=c=0，则y=ax2.以上三种形式都是二次函数的特殊形式，而y=ax2+bx+c（a≠0）是二次函数的一般式.二次函数由特殊到一般，可分为以下几种形式：①（a≠0）；②（a≠0）；③（a≠0）；④（a≠0），其中；⑤（a≠0）.要点诠释：如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．a的绝对值越大，抛物线的开口越小.2.二次函数解析式的表示方法1.一般式：2yaxbxc（a，b，c为常数，0a）；2.顶点式：2()yaxhk（a，h，k为常数，0a）；3.两根式：12()()yaxxxx（0a，1x，2x是抛物线与x轴两交点的横坐标）（或称交点式）.要点诠释：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x轴有交点，即240bac时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com要点二、二次函数y=ax2（a≠0）的图象及性质1.二次函数y=ax2(a≠0)的图象用描点法画出二次函数y=ax2（a≠0）的图象，如图，它是一条关于y轴对称的曲线，这样的曲线叫做抛物线.因为抛物线y=x2关于y轴对称，所以y轴是这条抛物线的对称轴，对称轴与抛物线的交点是抛物线的顶点，从图上看，抛物线y=x2的顶点是图象的最低点。因为抛物线y=x2有最低点，所以函数y=x2有最小值，它的最小值就是最低点的纵坐标.2.二次函数y=ax2(a≠0)的图象的画法用描点法画二次函数y=ax2（a≠0）的图象时，应在顶点的左、右两侧对称地选取自变量x的值，然后计算出对应的y值，这样的对应值选取越密集，描出的图象越准确.要点诠释：二次函数y=ax2(a≠0)的图象．用描点法画二次函数y=ax2(a≠0)的图象，该图象是轴对称图形，对称轴是y轴．y=ax2(a≠0)是最简单的二次函数，把y=ax2(a≠0)的图象左右、上下平行移动可以得到y=ax2+bx+c(a≠0)的图象．画草图时应抓住以下几点：开口方向，对称轴，顶点，与x轴的交点，与y轴的交点.3.二次函数y=ax2(a≠0)的图象的性质二次函数y=ax2（a≠0）的图象的性质，见下表：函数图象开口方向顶点坐标对称轴函数变化最大（小）值y=ax2a>0向上（0，0）y轴x>0时，y随x增大而增大；x<0时，y随x增大而减小.当x=0时，y最小=0小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comy=ax2a<0向下（0，0）y轴x>0时，y随x增大而减小；x<0时，y随x增大而增大.当x=0时，y最大=0要点诠释：顶点决定抛物线的位置.几个不同的二次函数，如果二次项系数a相同，那么抛物线的开口方向、开口大小完全相同，只是顶点的位置不同.│a│相同，抛物线的开口大小、形状相同.│a│越大，开口越小，图象两边越靠近y轴，│a│越小，开口越大，图象两边越靠近x轴.要点三、二次函数y=ax2+c(a≠0)的图象及性质1.二次函数y=ax2+c(a≠0)的图象（1）0a（2）0a2.二次函数y=ax2+c(a≠0)的图象的性质关于二次函数2(0)yaxca的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：函数2(0,0)yaxcac2(0,0)yaxcacjjjj小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图象开口方向向上向下顶点坐标(0，c)(0，c)对称轴y...