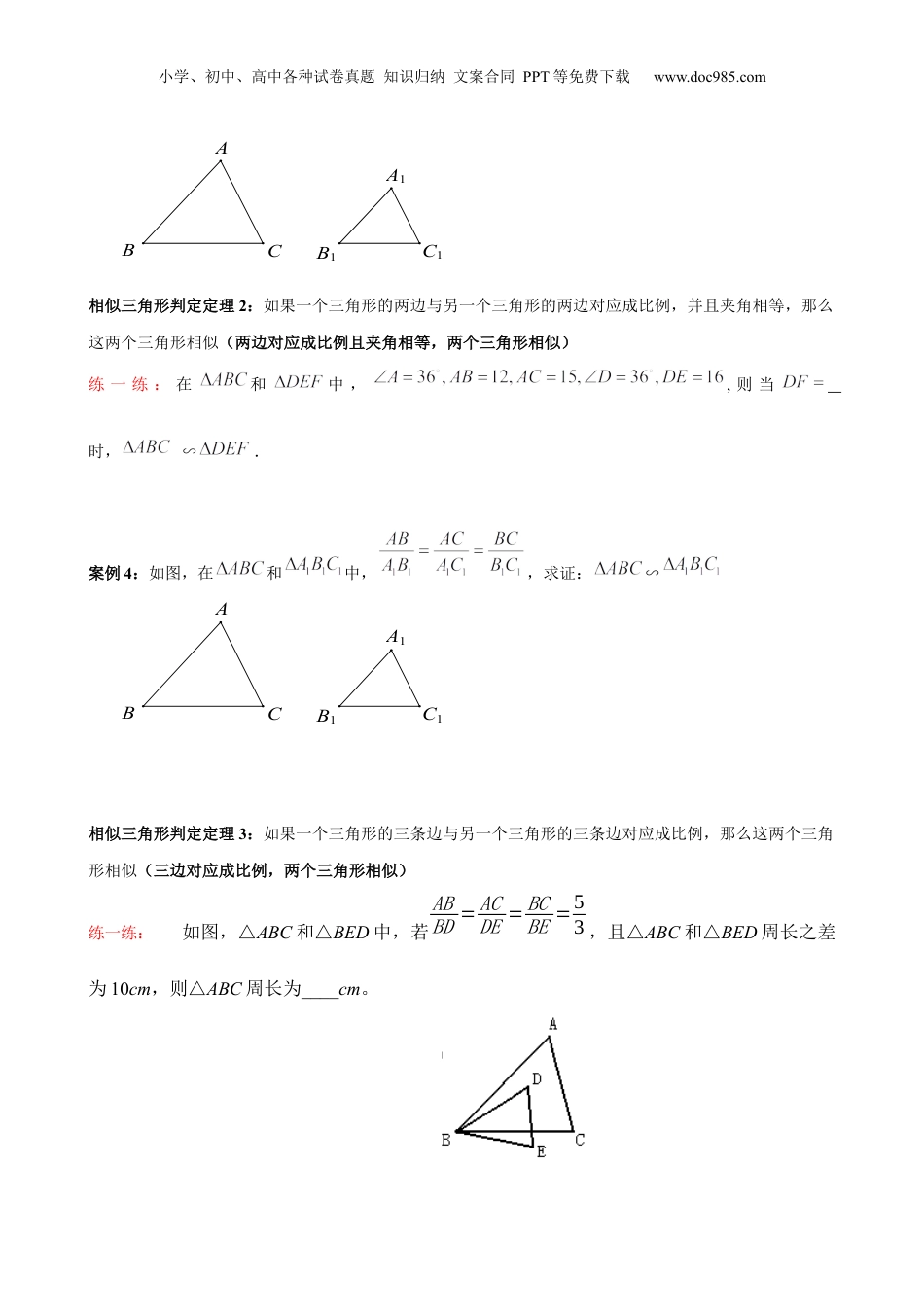
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第4讲相似三角形判定知识归纳思考：什么叫做全等三角形？两个全等三角形的对应边和对应角有什么关系？全等三角形的判断方法？概念辨析：如果一个三角形与另一个三角形的三个角对应相等、三边对应成比例的两个三角形，那么这两个三角形叫做相似三角形．如图，与是相似三角形，可记作∽，其中点与点，点与点，点与点分别是对应顶点，“∽“读作”相似于”；相似三角形对应边的比，叫做相似比（或相似系数）．C1ABCA1B1注意：①两个相似三角形的相似比具有顺序性．②全等三角形的相似比为1，这也说明了全等三角形是相似三角形的特殊情形．强调：在写两个三角形相似时，通常把表示对应顶点的字母写在对应位置上．思考：如果∽，∽，那么与相似吗？请同学们利用相似三角形的定义说理。归纳总结：相似三角形具有传递性，如果两个三角形分别与同一个三角形相似，那么这两个三角形也相似。练一练：1．如图，△ABC∽△DEC，其中点A与点D是对应顶点，请写出对应角和对应边成比例的比例式．2．如图，△ADE∽△ABC，其中点D与点B是对应顶点，请写出对应角和对应边成比例的比例式．CABEDABCED小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com案例1：通过学习三角形一边的平行线性质定理，如下图，分别在直线上，若，能否得到∽？lEDABClCBEDAlEDCBA相似三角形预备定理：平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似案例2：如图，在和中，，求证：∽C1B1ABCA1相似三角形判定定理1：如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似（两角对应相等，两个三角形相似）.练一练：如图，△ABC中，AB＝7，AD＝4，∠B＝∠ACD，则AC＝________。案例3：如图，在和中，，,，求证：∽小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC1B1ABCA1相似三角形判定定理2：如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似（两边对应成比例且夹角相等，两个三角形相似）练一练：在和中，,则当时，∽．案例4：如图，在和中，，求证：∽C1B1ABCA1相似三角形判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似（三边对应成比例，两个三角形相似）练一练：如图，△ABC和△BED中，若ABBD=ACDE=BCBE=53，且△ABC和△BED周长之差为10cm，则△ABC周长为____cm。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com相似三角形判定小结:相似三角形预备定理：平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似（平行即相似）相似三角形判定定理1：如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似（两角对应相等，两个三角形相似）.相似三角形判定定理2：如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似（两边对应成比例且夹角相等，两个三角形相似）相似三角形判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似（三边对应成比例，两个三角形相似）典型例题例题1：如图，在正方形网格上有两个三角形和，求证:∽试一试：如图，是一个正方形网络，里面有许多三角形．在下面所列出的各三角形中，与不相似的是()（A）△BDE（B）△BCD（C）△FGH（D）△BFG.例题3：在ABC中，3AB，4AC，D、E分别为AB、AC上一点，1AD，当AE取何值时，ADE与ABC相似.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com试一试:在正方形ABCD中，已知AB=6，点E在边CD上，且DE:CE=1:2，如图,点F在BC的延长线上，如果△ADE与点C、E、F所组成的三角形相似，那么CF=．例题4：已知：如图，在△中，，∥，点在边上，与相交于点，且∠=∠．求证：（1）△∽△；（2）．试一试：已知，如图，在Rt△ABC中，AB=AC，∠DAE=45°．求证：（1）△ABE∽△DCA；（2）EDCABEDCBAGFEDACB小学、初中、高中各...