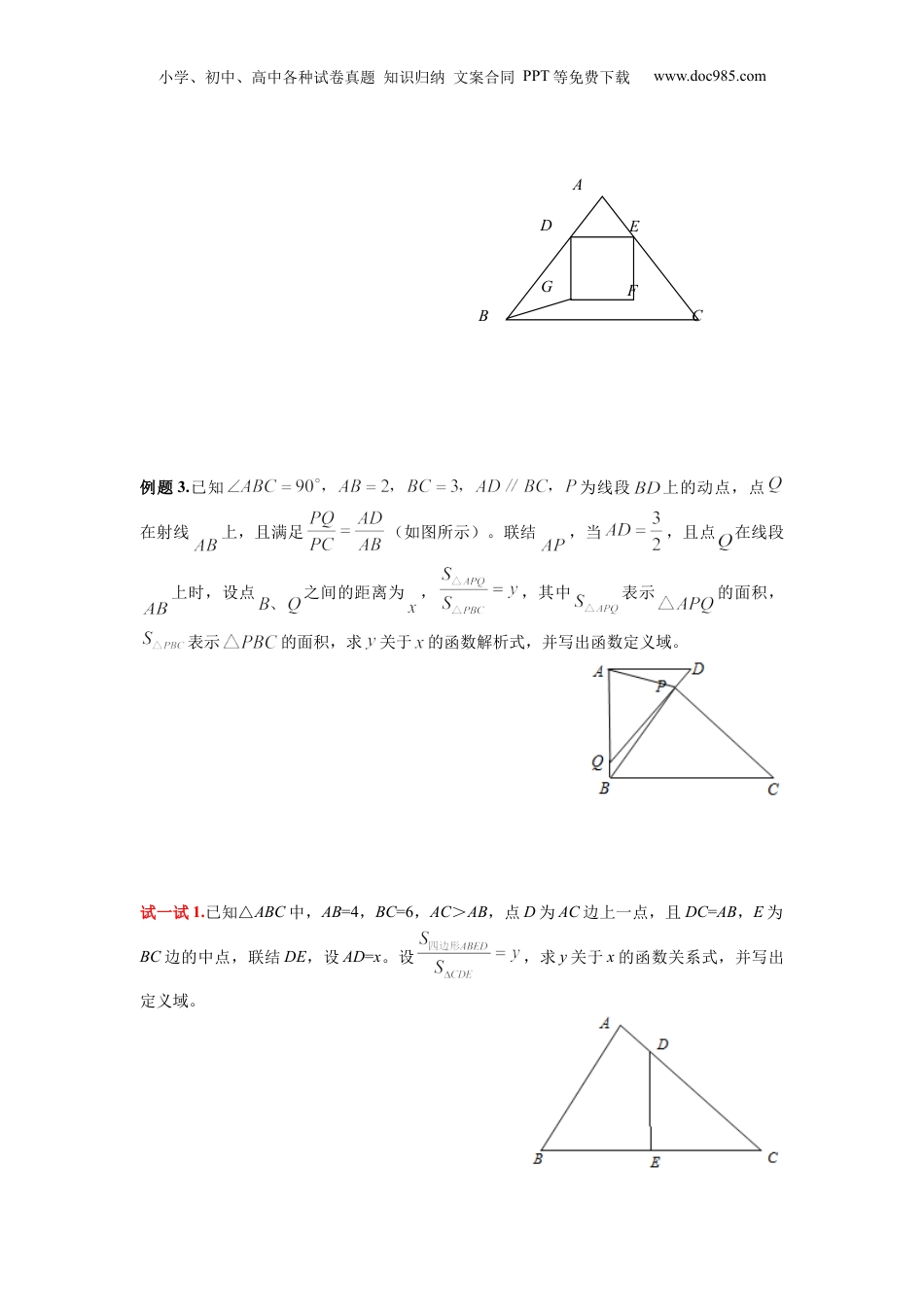
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第11讲相似中的面积问题知识归纳一.求图形面积类型：其形它图面积影部分阴面积重部分叠面积四形边面积三角形面积求形面图积种类二．三角形面积的一般求解方法：4.用面比求积：同底的三角形面之比等于高之积比，同高的三角形面之比等于底之比积边3.用相似三角形求解：相似三角形的面之比等于相似比的平方积2.分割法和法拼凑1.直接求：三角形面积的求解方法典型例题例题1.已知，，（如图）．是射线上的动点（点与点不重合），是线段的中点。设，的面积为，求关于的函数解析式，并写出函数的定义域。备用图CDABCEMDAB小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例题2.如图，在直角梯形ABCD中，AD∥BC，∠A=90o，BD⊥DC，BC=10cm，CD=6cm．在线段BC、CD上有动点F、E，点F以每秒2cm的速度，在线段BC上从点B向点C匀速运动；同时点E以每秒1cm的速度，在线段CD上从点C向点D匀速运动．当点F到达点C时，点E同时停止运动．设点F运动的时间为t（秒）．（1）求AD的长；（2）设四边形BFED的面积为y，求y关于t的函数关系式，并写出函数定义域；面积关系的解题方法和策略：1.注意题目中的已知量和特殊条件；2.找到：动点、自变量、所求图形面积；3.观察所求图形面积是否可以直接求解，如不能，则添加辅助线或利用面积转化求解；4.注意求解面积的一般方法：直接法、面积和差关系、比例法等求解；5.利用好以下定理：勾股定理、相似三角形的性质等试一试.如图，在ΔABC中，AB=AC=5,BC=6，D、E分别是边AB、AC上的两个动点（D不与A、B重合），且保持DE∥BC，以DE为边，在点A的异侧作正方形DEFG.（1）试求ΔABC的面积；（2）当边FG与BC重合时，求正方形DEFG的边长；（3）设AD=x，ΔABC与正方形DEFG重叠部分的面积为y，试求y关于x的函数关系式，并写出定义域。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例题3.已知为线段上的动点，点在射线上，且满足（如图所示）。联结，当，且点在线段上时，设点之间的距离为，，其中表示的面积，表示的面积，求关于的函数解析式，并写出函数定义域。试一试1.已知△ABC中，AB=4，BC=6，AC＞AB，点D为AC边上一点，且DC=AB，E为BC边的中点，联结DE，设AD=x。设，求y关于x的函数关系式，并写出定义域。ABCDEFG小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com试一试2.如图，已知在直角梯形中，∥，，，，．动点、分别在边和上，且．线段与相交于点，过点作∥，交于点，射线交的延长线于点，设．（1）求DFCF的值。（2）当点运动时，试探究四边形的面积是否会发生变化？如果发生变化，请用的代数式表示四边形的面积；如果不发生变化，请求出这个四边形的面积。课上习题1：如图所示，在直角梯形ABCD中，∥，点E在BC上，点F在AC上，（1）求证：∽；（2）当AD=8，DC=6，点E，F分别是BC，AC的中点时。求直角梯形ABCD的面积2.如图，已知矩形，，，现将一把三角尺放在矩形上，并使它的直角顶点在对角线上滑动（点与、两点不重合），两条直角边分别DPEFGCQBA（例2题图）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comFEACDB交线段、于点、，且、．设的长为。（1）求线段、的长；（用含的代数式表示）（2）过点作，交线段于点。①如点在线段上（点不与点重合），设四边形的面积为，求关于的函数解析式，并写出函数的定义域；②当时，求的长。FEADCBPFEADCBPH（图1）（图2）课后作业1．在△中，是的中点，且，⊥，与相交于点，与相交于点．（1）求证：△∽△；（2）若，，求△的面积．2.己知分别是△的边、上的高，高、所在的直线相交于点。(如图)（1）当是锐角时，求证：△∽△；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）当是钝角时，（1）中的结论还成立吗？直接写出结论，无需说明理由；（3）如果,求的值。3.如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12。设E在AD上，AE=2，F为AB上一个动点（不与A、B重合），过F作FG∥EC，交BC于...