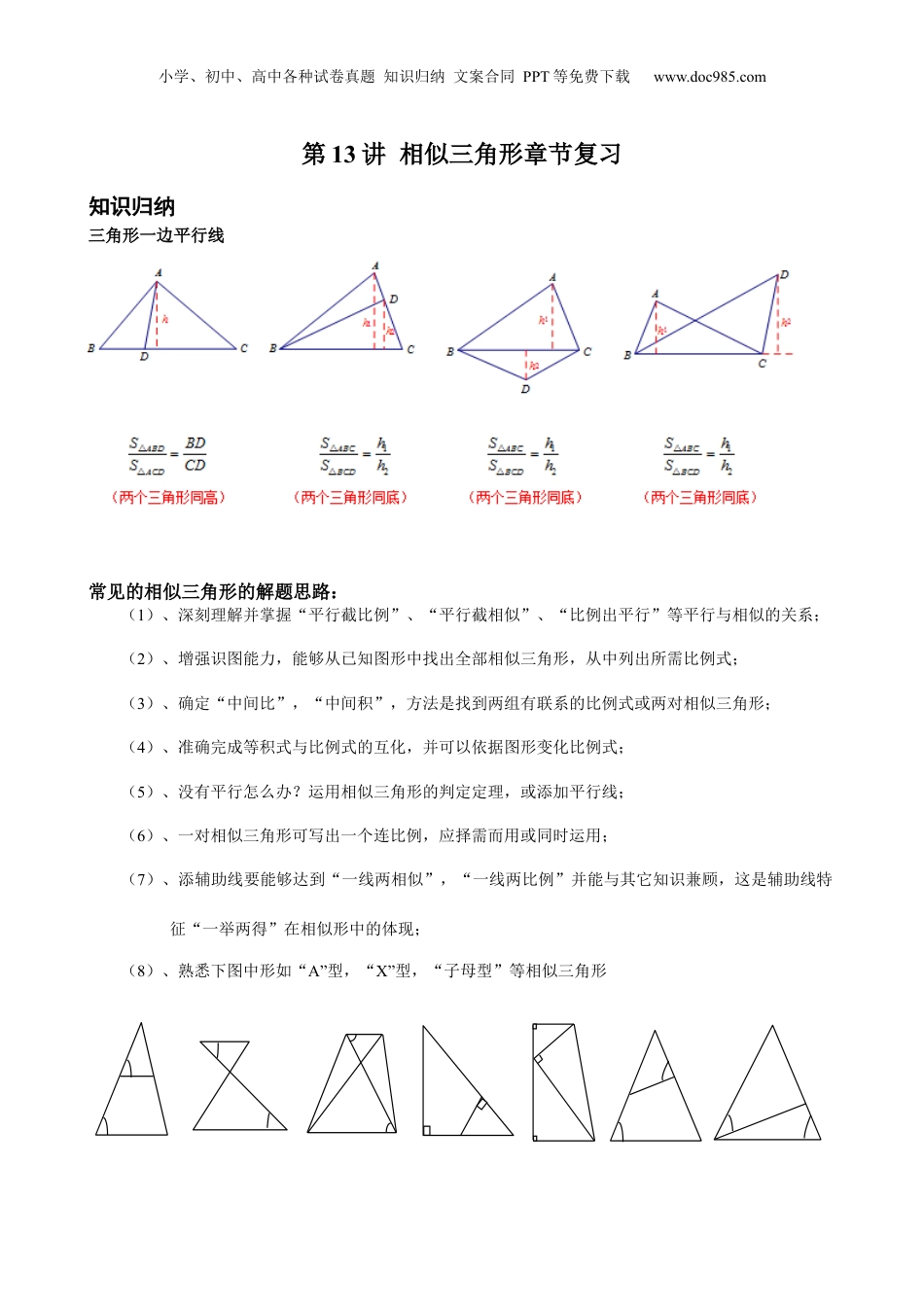
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第13讲相似三角形章节复习知识归纳三角形一边平行线常见的相似三角形的解题思路：（1）、深刻理解并掌握“平行截比例”、“平行截相似”、“比例出平行”等平行与相似的关系；（2）、增强识图能力，能够从已知图形中找出全部相似三角形，从中列出所需比例式；（3）、确定“中间比”，“中间积”，方法是找到两组有联系的比例式或两对相似三角形；（4）、准确完成等积式与比例式的互化，并可以依据图形变化比例式；（5）、没有平行怎么办？运用相似三角形的判定定理，或添加平行线；（6）、一对相似三角形可写出一个连比例，应择需而用或同时运用；（7）、添辅助线要能够达到“一线两相似”，“一线两比例”并能与其它知识兼顾，这是辅助线特征“一举两得”在相似形中的体现；（8）、熟悉下图中形如“A”型，“X”型，“子母型”等相似三角形小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典型例题知识点一（相似三角形的判定）要点1：相似三角形（1）如果两个三角形的三个角对应相等、三边对应成比例，那么这两个三角形叫做相似三角形.两个三角形相似，用符号“∽”表示，符号“∽”读作“相似于”（2）相似三角形的对应角相等、对应边成比例.两个相似三角形的对应边的比，叫做这两个三角形的相似比（或相似系数），一般用表示，当时，这两个相似三角形就成为全等三角形.全等三角形是相似三角形的特例要点2：相似三角形的传递性如果△ABC∽△A1B1C1，△A1B1C1∽△A2B2C2，那么△ABC∽A2B2C2要点3：相似三角形的判定定理（相似三角形与全等三角形判定方法的联系）全等的判定SASSSSAAS(ASA)直角三角形HL相似的判定两边成比例夹角相等三边对应成比例两角相等一直角边与斜边对应成比例例1.在和中，，，根据下列条件，能判断和相似的是（）（A）；（B）；（C）；（D）；【答案】B例2.在△ABC中，点D、E分别在边BA、CA的延长线上（如图），下列四个选项中，能判定DE∥BC的是（）A、B、C、D、AEDBC【答案】B小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1.如图，已知是△中的边上的一点，，的平分线交边于，交于，那么下列结论中错误的是（）A.△△∽B.△∽△C.△∽△【答案】A2.如图，△在边长为1个单位的方格纸中，它们的顶点在小正方形顶点位置，点、、、、也是小正方形的顶点，从点、、、、中选取三个点所构成的三角形与△相似，那么这个三角形是【答案】△3.“相似的图形”是（）（A）形状相同的图形；（B）大小不相同的图形；（C）能够重合的图形；（D）大小相同的图形．【答案】A4、如图，在四边形中，如果，那么下列条件中不能判定和相似的是（）（A）;（B）是的平分线；（C）;（D）【答案】C5.在△ABC中，点D、E分别在边AB、AC上，联结DE，那么下列条件中不能判断ADE△和△ABC相似的是（）图2BCAD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA、DE∥BCB、∠AED=∠BC、D、【答案】D6.下列命题不一定成立的是（）A.斜边与一条直角边对应成比例的两个直角三角形相似B.两个等腰直角三角形相似C.两边对应成比例且有一个角相等的两个三角形相似D.各有一个角等于100°的两个等腰三角形相似【答案】C7.如图，在△中，，，，是边的中点，现有一点位于边上，使得△与△相似，则线段的长为【答案】或8.如图，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB;③ACCD=ABBC④AC2=AD⋅AB,其中不能判定△ABC～△ACD的条件为（）A.①B.②C.③D.④【答案】C二、知识点二（相似三角形的性质）相似三角形的性质定理1：相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.相似三角形的性质定理2：相似三角形周长比等于相似比．相似三角形的性质定理3：相似三角形的面积比等于相似比的平方．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识架构图例1.如果两个相似三角形的相似比是1:4，那么它们的面积比是；【答案】例2.如果两个相似三角形对应角平分线的比是4：9，那么这两个三角形的周长比...