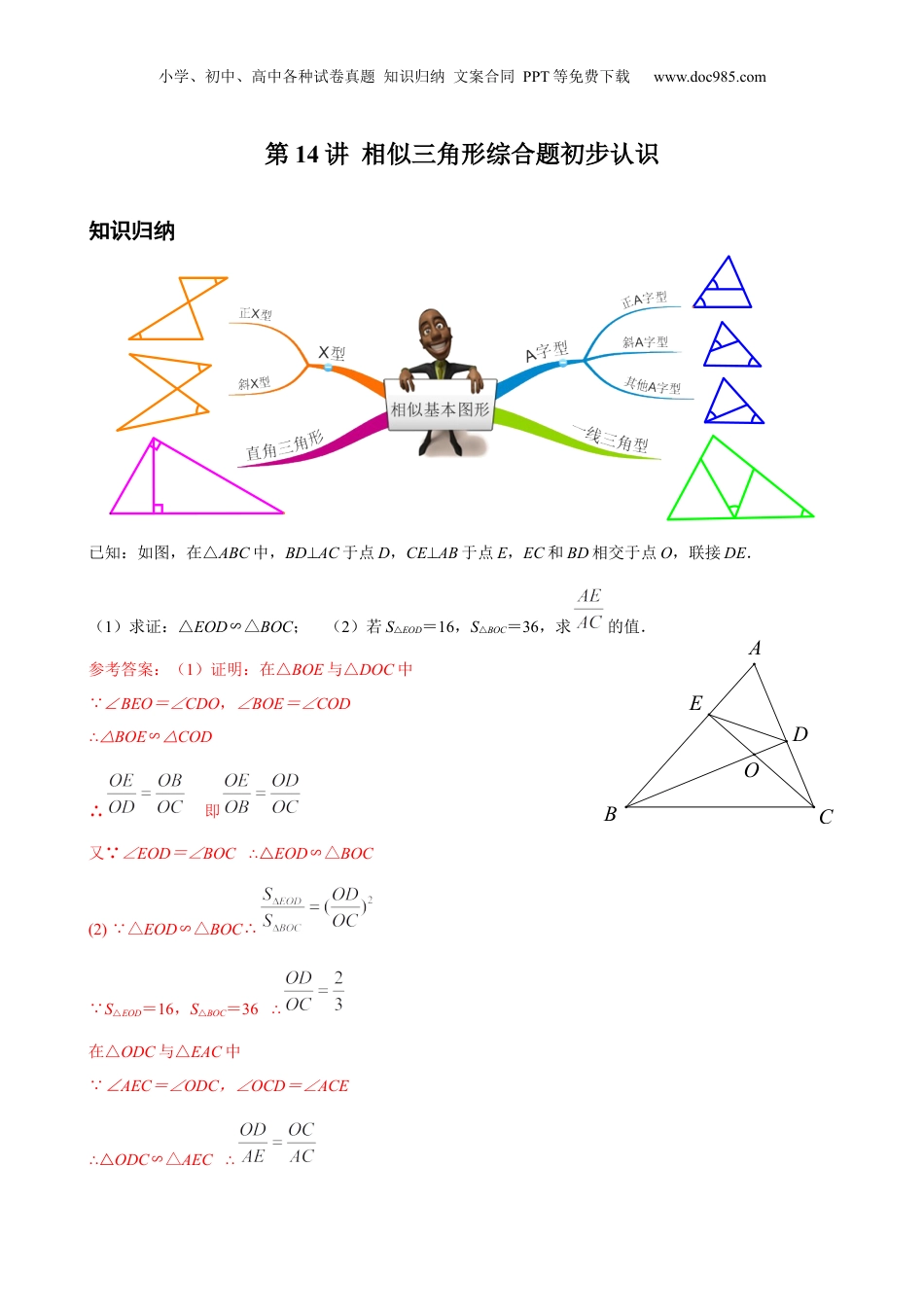
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第14讲相似三角形综合题初步认识知识归纳已知：如图，在△ABC中，BD⊥AC于点D，CE⊥AB于点E，EC和BD相交于点O，联接DE．（1）求证：△EOD∽△BOC；（2）若S△EOD＝16，S△BOC＝36，求的值．参考答案：（1）证明：在△BOE与△DOC中 BEO∠＝∠CDO，∠BOE＝∠COD∴BOE△∽COD△∴即又 ∠EOD＝∠BOC∴△EOD∽△BOC(2) △EOD∽△BOC∴ S△EOD＝16，S△BOC＝36∴在△ODC与△EAC中 AEC∠＝∠ODC，∠OCD＝∠ACE∴△ODC∽△AEC∴ODEBCA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com即∴问题1：上题中如何证明△ADE∽△ABC？参考答案：先证△ABD∽△ACE，再根据两边对于成比例且夹角相等即可。问题2：上题中共有多少对相似三角形？参考答案：8对典型例题例题1：如图，在△ABC中，D是AB的中点，过点D的直线交边AC于点E，交BC的延长线于点F，求证：．EBFACD教学说明：此题考查三角形一边的平行线性质定理推论；注意讲解此类题作平行线的不同方法；证明：如图，过点C作CG∥AB，交DF于点G． CG∥AD，∴，同理：，又 AD=BD，∴，∴∴GEBFACD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com试一试：如图，直线BD交AC、AB于D、F，交CB的延长线于E，且，．求的值．FECABD参考答案：如图，过点D作DG∥BC，交AB于点G，则有，又 ，∴设AF=7k，FB=3k，则AB=10k，于是AG=4k，GF=3k，∴．例题2：已知：如图，正方形ABCD的边长是1，P是CD的中点，点Q是线段BC上一动点，当BQ为何值时，以A,D,P为顶点的三角形与以Q,C,P为顶点的三角形相似．DACBPQ分析：△ADP与△QCP相似时，∠D=∠C=90°，分两种情况讨论解： 正方形ABCD的边长是1，P是CD的中点，∴PD=PC=GFECABD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com①当∠DPA=∠CPQ时，，即，解得CQ=1，∴；②当∠DPA=∠PQC时，，，解得，∴试一试：如图，在正方形ABCD中，E为BC中点，点F在CD边上，且DF=3FC，联结AE、AF、EF，图中是否存在与∠EAF相等的角？若存在，请写出并加以证明；若不存在，请说明理由．参考答案：图中存在与相等的角，分别是和由正方形ABCD得， E为BC中点，DF=3FC，∴，，∴在和中， 且∴∽．∴，且在中 ，∴∴，∴，又 ，∴∽，∴同理．例题3：如图，已知在中，，于，是的中点，的延长线FCEBDADEA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com与的延长线交于点．（1）求证：△FDC∽△FBD；（2）求证：．证明：（1） ，∴∠ACD+∠DCB=∠B=∠DCB=90°∴∠ACD=∠B 是的中点∴DE=EC∴∠ACD=∠FDC∴∠FCD=∠B∴△FDC∽△FBD(2) △FDC∽△FBD∴ 在和中，∴试一试：如图，梯形中，，，点在边上，与相交于点，且．求证：（1）∽；（2）．证明：（1）在梯形中， ，∴ ，∴△∽△∴ OEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴△∽△证明：（2） △∽△，∴ ∴△∽△∴∴∴例题4：如图所示，在直角梯形ABCD中，∥，点E在BC上，点F在AC上，（1）求证：∽；（2）当AD=8，DC=6，点E，F分别是BC，AC的中点时。求直角梯形ABCD的面积解：（1）在梯形ABCD中，∥∴∠DAF=∠ACE又 ∠DFC=∠AEB，∠DFC=∠DAF+∠ADF，∠AEB=∠ACE+∠CAE∴∠ADF=∠CAE，∴∽（2） AD=8，DC=6，，∴AC=10，又 F是AC的中点，∴AF=5，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com ∽，∴,∴CE=. E是BC的中点，∴BC=,∴直角梯形ABCD的面积=（+8）6=课上习题1．如图：四边形对角线与相交于点，，．（1）求证：∽；（2）点在线段上，若∥，求证：．证明：（1） ，，∴.又，∴∽.（2）由（1）得：∽.∴. ∥，∴.∴. ，∴∽.∴.∴.2．如图，在矩形中，，，点是线段上的一个动点，将三角板的直角顶点重EOCBAD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com合于点，三角板两直角中的一边始终经过点，另一直角边交射线于点．（1）证明：△∽△；（2）设，，求与的函数...