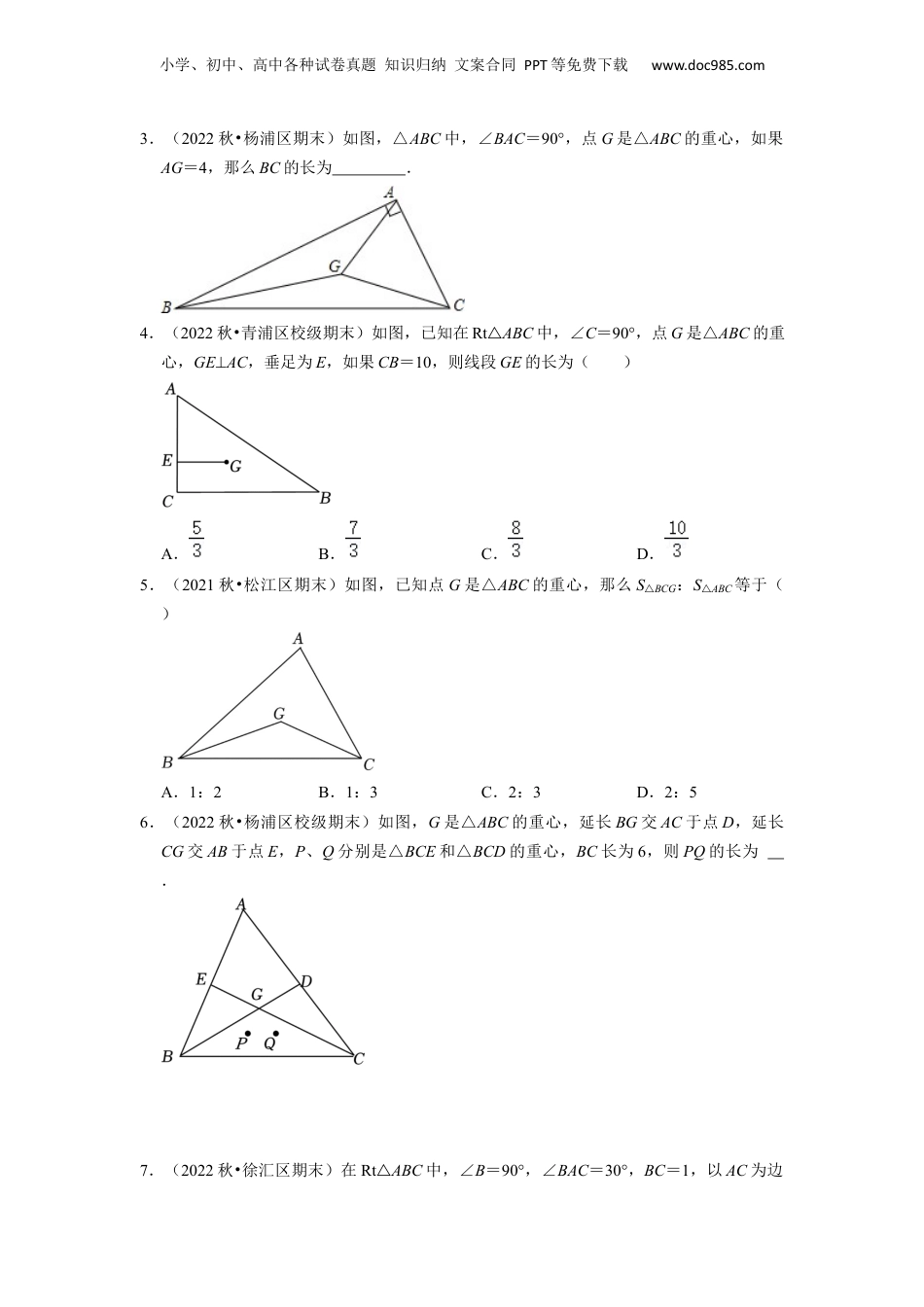
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第03讲三角形一边的平行线【知识梳理】1、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线，截得的对应线段成比例．如图，已知，直线，且与、所在直线交于点和点，那么．2、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原三角形的三边对应成比例．如图，点、分别在的边、上，，那么．3、三角形的重心定义：三角形三条中线交于一点，三条中线交点叫三角形的重心．性质：三角形重心到一个顶点的距离，等于它到这个顶点对边中点的距离的两倍．4、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例，那么这条直线平行于三角形的第三边．5、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线（这两边的延长线在第三边的同侧）所得的对应小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com线段成比例，那么这条直线平行于三角形的第三边．如图，在中，直线与、所在直线交于点和点，如果那么//．6、平行线分线段成比例定理两条直线被三条平行的直线所截，截得的对应线段成比例．如图，直线////，直线与直线被直线、、所截，那么．7、平行线等分线段定理两条直线被三条平行的直线所截，如果一条直线上截得的线段相等，那么另一条直线上截得的线段也相等．【考点剖析】一．三角形的重心（共13小题）1．（2023•青浦区一模）三角形的重心是（）A．三角形三条角平分线的交点B．三角形三条中线的交点C．三角形三条边的垂直平分线的交点D．三角形三条高的交点2．（2023•奉贤区一模）在△ABC中，AD是BC边上的中线，G是重心．如果AD＝6，那么线段DG的长是．GFEDCB小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3．（2022秋•杨浦区期末）如图，△ABC中，∠BAC＝90°，点G是△ABC的重心，如果AG＝4，那么BC的长为．4．（2022秋•青浦区校级期末）如图，已知在Rt△ABC中，∠C＝90°，点G是△ABC的重心，GE⊥AC，垂足为E，如果CB＝10，则线段GE的长为（）A．B．C．D．5．（2021秋•松江区期末）如图，已知点G是△ABC的重心，那么S△BCG：S△ABC等于（）A．1：2B．1：3C．2：3D．2：56．（2022秋•杨浦区校级期末）如图，G是△ABC的重心，延长BG交AC于点D，延长CG交AB于点E，P、Q分别是△BCE和△BCD的重心，BC长为6，则PQ的长为．7．（2022秋•徐汇区期末）在Rt△ABC中，∠B＝90°，∠BAC＝30°，BC＝1，以AC为边小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在△ABC外作等边△ACD，设点E、F分别是△ABC和△ACD的重心，则两重心E与F之间的距离是．8．（2022秋•黄浦区月考）已知点G是△ABC的重心，那么S△ABG：S△ABC＝．9．（2023•金山区一模）如图，△ABC为等腰直角三角形，∠A＝90°，AB＝6，G1为△ABC的重心，E为线段AB上任意一动点，以CE为斜边作等腰Rt△CDE（点D在直线BC的上方），G2为Rt△CDE的重心，设G1、G2两点的距离为d，那么在点E运动过程中d的取值范围是．10．（2023•松江区一模）已知△ABC，P是边BC上一点，△PAB、△PAC的重心分别为G1、G2，那么的值为．11．（2022秋•徐汇区期中）已知点G是等腰直角三角形ABC的重心，AC＝BC＝6，那么AG的长为．12．（2018•宝山区校级自主招生）G为重心，DE过重心，S△ABC＝1，求S△ADE的最值，并证明结论．13．（2019秋•嘉定区校级月考）如图，点G是△ABC的重心，过点G作EF∥BC，分别交AB、AC于点E、F，且EF+BC＝7.2cm，求BC的长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二．平行线分线段成比例（共19小题）14．（2022秋•徐汇区期末）在△ABC中，点D、E分别在边AB和BC上，AD＝2，DB＝3，BC＝10，要使DE∥AC，那么BE必须等于．15．（2022秋•闵行区期末）如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、C、E和点B、D、F，如果AC：CE＝3：1，BF＝10，那么DF等于（）A．B．C．D．16．（2023•宝山区一模）在△ABC中，点D...