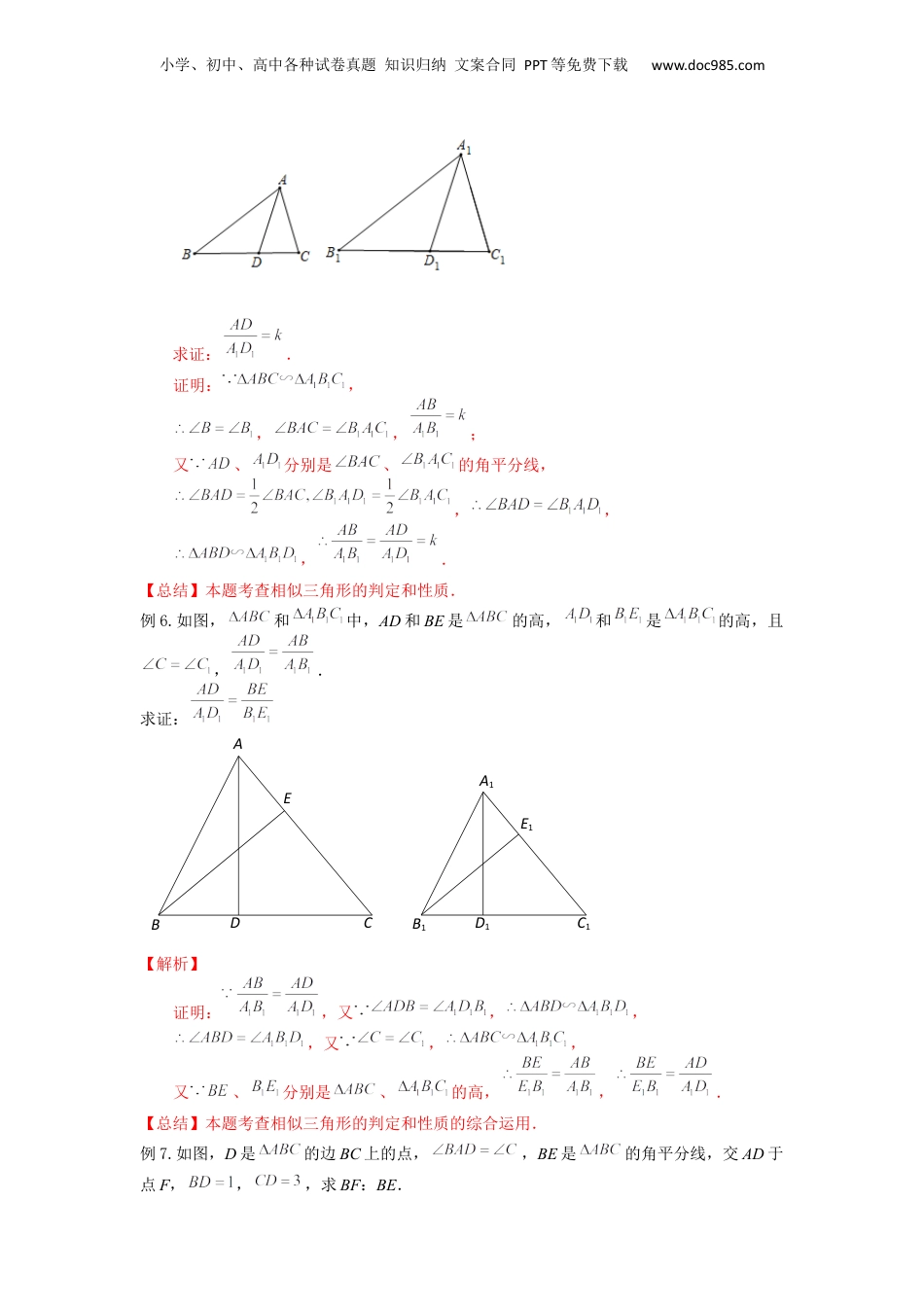
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第05讲相似三角形的性质定理（3种题型）【知识梳理】一、相似三角形性质定理1相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比．二、相似三角形性质定理2相似三角形周长的比等于相似比．三、相似三角形性质定理3相似三角形的面积的比等于相似比的平方．【考点剖析】题型一：相似三角形性质定理1例1.已知∽，顶点A、B、C分别与A1、B1、C1对应，，BE、B1E1分别是它们的对应中线，且．求B1E1的长．【答案】4．【解析】解：，、分别是对应中线，即，【总结】本题考查相似三角形对应中线的比等于相似比．例2.已知∽，顶点A、B、C分别与A1、B1、C1对应，，,的平分线A1D1的长为6，求的平分线的长．【答案】8．【解析】解：，、分别是、的平分线，即，即的平分线的长为8．【总结】本题考查相似三角形对应角平分线的比等于相似比．例3.求证：相似三角形对应高的比等于相似比．【解析】已知：如图，，且相似比为，、分别是、的高．求证：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com证明：，，；又、分别是、的高，，，．【总结】本题考查相似三角形的判定和性质．例4.求证：相似三角形对应中线的比等于相似比．【解析】已知：如图，，且相似比为，、分别是边、的中线．求证：．证明：，，；又、分别是边、的中线，，，，，，．【总结】本题考查相似三角形的判定和性质的运用．例5.求证：相似三角形对应角平分线的比等于相似比．【解析】已知：如图，，且相似比为，、分别是、的角平分线．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com求证：．证明：，，，；又、分别是、的角平分线，，，，．【总结】本题考查相似三角形的判定和性质．例6.如图，和中，AD和BE是的高，和是的高，且，．求证：【解析】证明：，又，，，又，，又、分别是、的高，，．【总结】本题考查相似三角形的判定和性质的综合运用．例7.如图，D是的边BC上的点，，BE是的角平分线，交AD于点F，，，求BF：BE．B1C1D1E1A1EDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】解：是的角平分线，，又，，，又，，，，，，．【总结】本题考查相似三角形的判定和性质的综合运用．例8.如图，在中，矩形DEFG的一边DE在BC边上，顶点G、F分别在AB、AC边上，AH是BC边上的高，AH与GF交于点K．若，，矩形DEFG的周长为76cm，求矩形DEFG的面积．【答案】．【解析】解：设，矩形，，,又是高，，,，,，，，，．【总结】本题考查三角形一边的平行线定理，矩形的周长面积等知识．例9.如图，正方形DEFG的边EF在的边BC上，顶点D、G分别在边AB、AC上，AH是的高，BC=60厘米，AH=40厘米，求正方形DEFG的边长．FEDCBAKHGFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】24．【解析】设正方形的边长为x，，．，，∴正方形的边长为24．【总结】本题考查三角形内接正方形的相关知识，主要还是通过比例相等来列式建立关系．例10.在锐角中，矩形DEFG的顶点D在AB边上，顶点E、F在BC边上，顶点G在AC边上，如果矩形DEFG的长为6，宽为4，设底边BC上的高为x，的面积为y，求y与x的函数关系式．【答案】．【解析】解：如图， 矩形，，．又 AH是高，．，，，PHGFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，，，又 ，∴．【总结】本题考查三角形一边的平行线定理，矩形的面积等知识．题型二：相似三角形性质定理2例11.若∽，与的相似比为1:2，则与的周长比为()（A）1:4（B）1:2（C）2:1（D）【答案】B【总结】相似三角形的周长比等于相似比．例12.已知∽，顶点A、B、C分别与A1、B1、C1对应，它们的周长分别为48和60，且，，求BC和A1B1的长．【答案】．【解析】解：，；又，．【总结】本题考查相似三角形的性质．例13.如果两个相似三角形的最长边分别为35厘米和14厘米，它们的周长相差60厘米，那么大三角形的周长是．【答案】．【解析】两三角形的相似比为，则周长比为，设大三角形周...