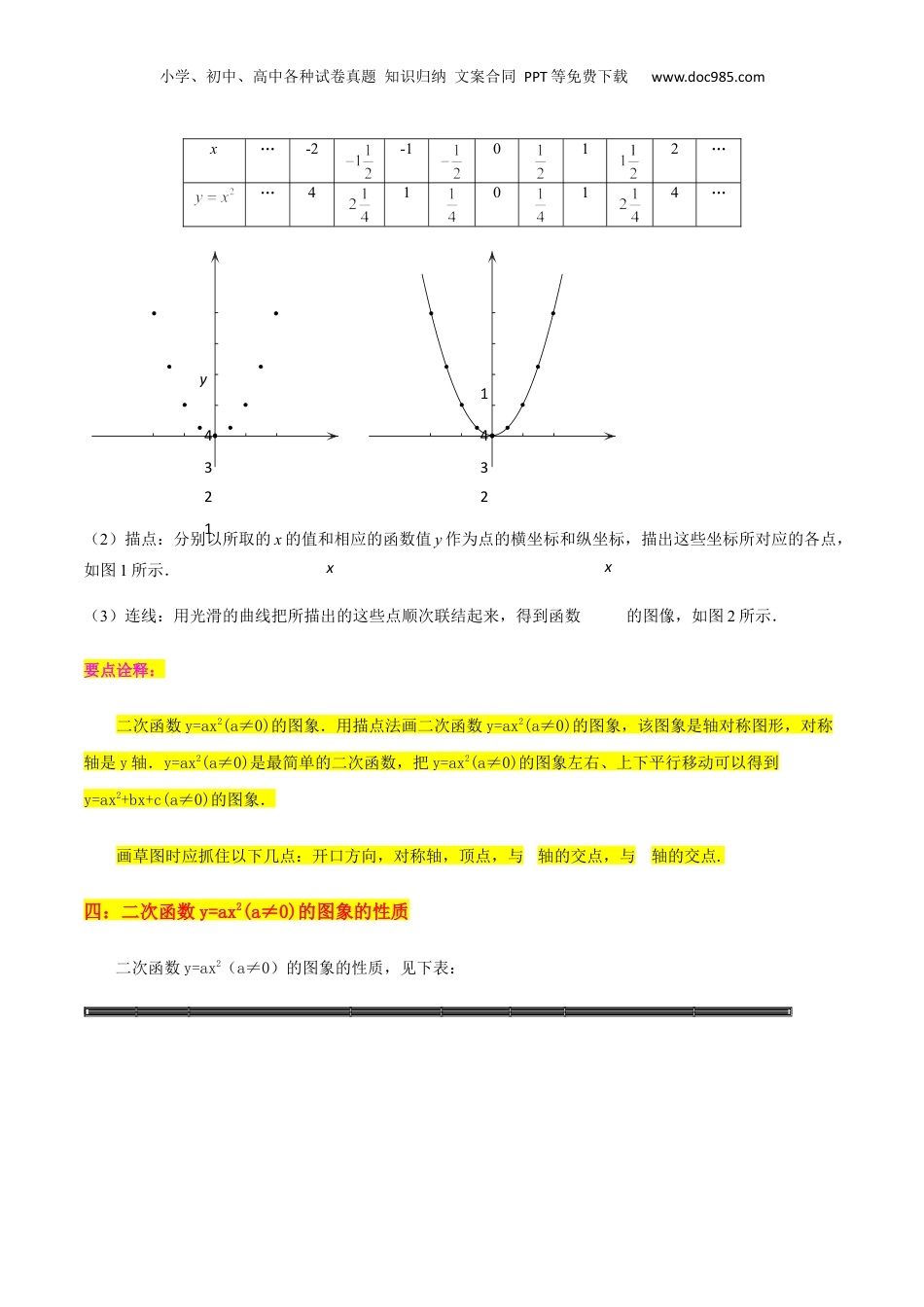
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第09讲二次函数的概念与y=ax2(a≠0)的图象和性质（10种题型）【知识梳理】一、二次函数的定义1.二次函数的定义：一般地，形如y＝ax2+bx+c（a、b、c是常数，a≠0）的函数，叫做二次函数．其中x、y是变量，a、b、c是常量，a是二次项系数，b是一次项系数，c是常数项．y═ax2+bx+c（a、b、c是常数，a≠0）也叫做二次函数的一般形式．判断函数是否是二次函数，首先是要看它的右边是否为整式，若是整式且仍能化简的要先将其化简，然后再根据二次函数的定义作出判断，要抓住二次项系数不为0这个关键条件．2.二次函数的取值范围：一般情况下，二次函数中自变量的取值范围是全体实数，对实际问题，自变量的取值范围还需使实际问题有意义．要点诠释：如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．a的绝对值越大，抛物线的开口越小.二、二次函数y=ax2(a≠0)的图象用描点法画出二次函数y=ax2（a≠0）的图象，如图，它是一条关于y轴对称的曲线，这样的曲线叫做抛物线.因为抛物线y=x2关于y轴对称，所以y轴是这条抛物线的对称轴，对称轴与抛物线的交点是抛物线的顶点，从图上看，抛物线y=x2的顶点是图象的最低点。因为抛物线y=x2有最低点，所以函数y=x2有最小值，它的最小值就是最低点的纵坐标.三、二次函数y=ax2(a≠0)的图象的画法在平面直角坐标系xOy中，按照下列步骤画二次函数的图像．（1）列表：取自变量x的一些值，计算相应的函数值y，如下表所示：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comx…-2-1012……41014…（2）描点：分别以所取的x的值和相应的函数值y作为点的横坐标和纵坐标，描出这些坐标所对应的各点，如图1所示．（3）连线：用光滑的曲线把所描出的这些点顺次联结起来，得到函数的图像，如图2所示．要点诠释：二次函数y=ax2(a≠0)的图象．用描点法画二次函数y=ax2(a≠0)的图象，该图象是轴对称图形，对称轴是y轴．y=ax2(a≠0)是最简单的二次函数，把y=ax2(a≠0)的图象左右、上下平行移动可以得到y=ax2+bx+c(a≠0)的图象．画草图时应抓住以下几点：开口方向，对称轴，顶点，与轴的交点，与轴的交点.四：二次函数y=ax2(a≠0)的图象的性质二次函数y=ax2（a≠0）的图象的性质，见下表：xyx43214321小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式5】下列函数中（x，t为自变量），哪些是二次函数？如果是二次函数，请指出二次项、一次项系数及常数项．（1）；（2）；（3）；（4）．【变式6】已知函数．（1）当m为何值时，这个函数是二次函数？（2）当m为何值时，这个函数是一次函数？【变式7】．如图，有一矩形纸片，长、宽分别为8厘米和6厘米，现在长宽上分别剪去宽为x厘米（）的纸条，则剩余部分（图中阴影部分）的面积y关于x的函数关系式为____________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式8】某公司4月份的营收为80万元，设每个月营收的增长率相同，且为x()，6月份的营收为y万元，写出y关于x的函数解析．【变式9】用长为15米的篱笆，一面靠墙（墙的长度超过15米），围成一个矩形花圃．设花圃的宽为x米，面积为y平方米，求y与x的函数解析式及函数的定义域．【变式10】三角形的两边长的和为10厘米，它们的夹角为30°，设其中一条边长为x厘米，三角形的面积为y平方厘米，试写出y与x之间的函数解析式及定义域．【变式11】设，与成反比例，与成正比例，则y与x的函数关系是（）A．正比例函数B．反比例函数C．二次函数D．一次函数【变式12】已知正方形的周长是C厘米，面积是S平方厘米．（1）求S关于C的函数关系式；（2）当S=1平方厘米，求正方形的边长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例2.已知二次函数的图像经过点Q（-1，-2），求a的值，并写出它的解析式．在平面直角坐标系中，画出它的图像．【变式】二次函数的图像是______，它的对称轴是______，顶点坐标是__...