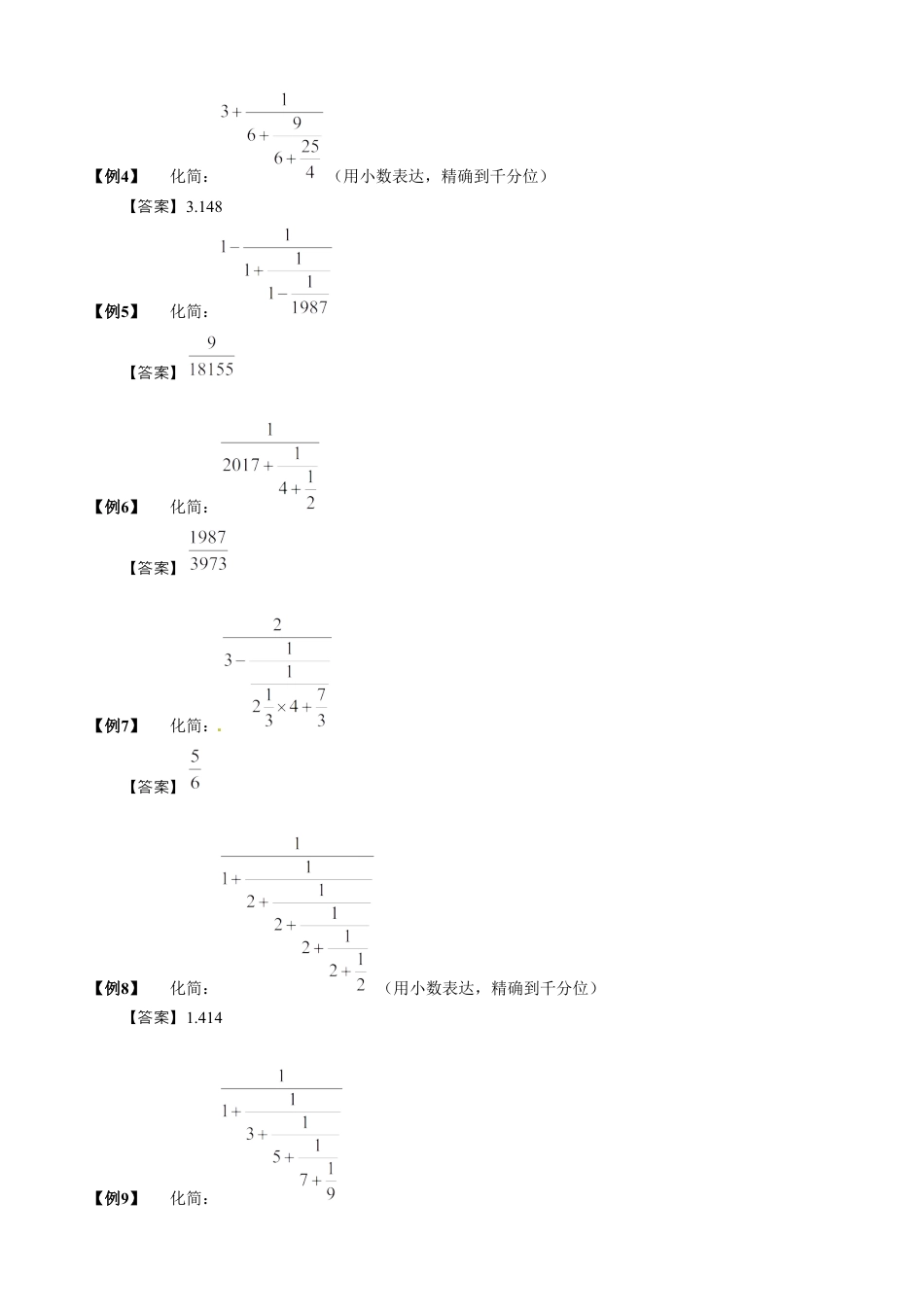
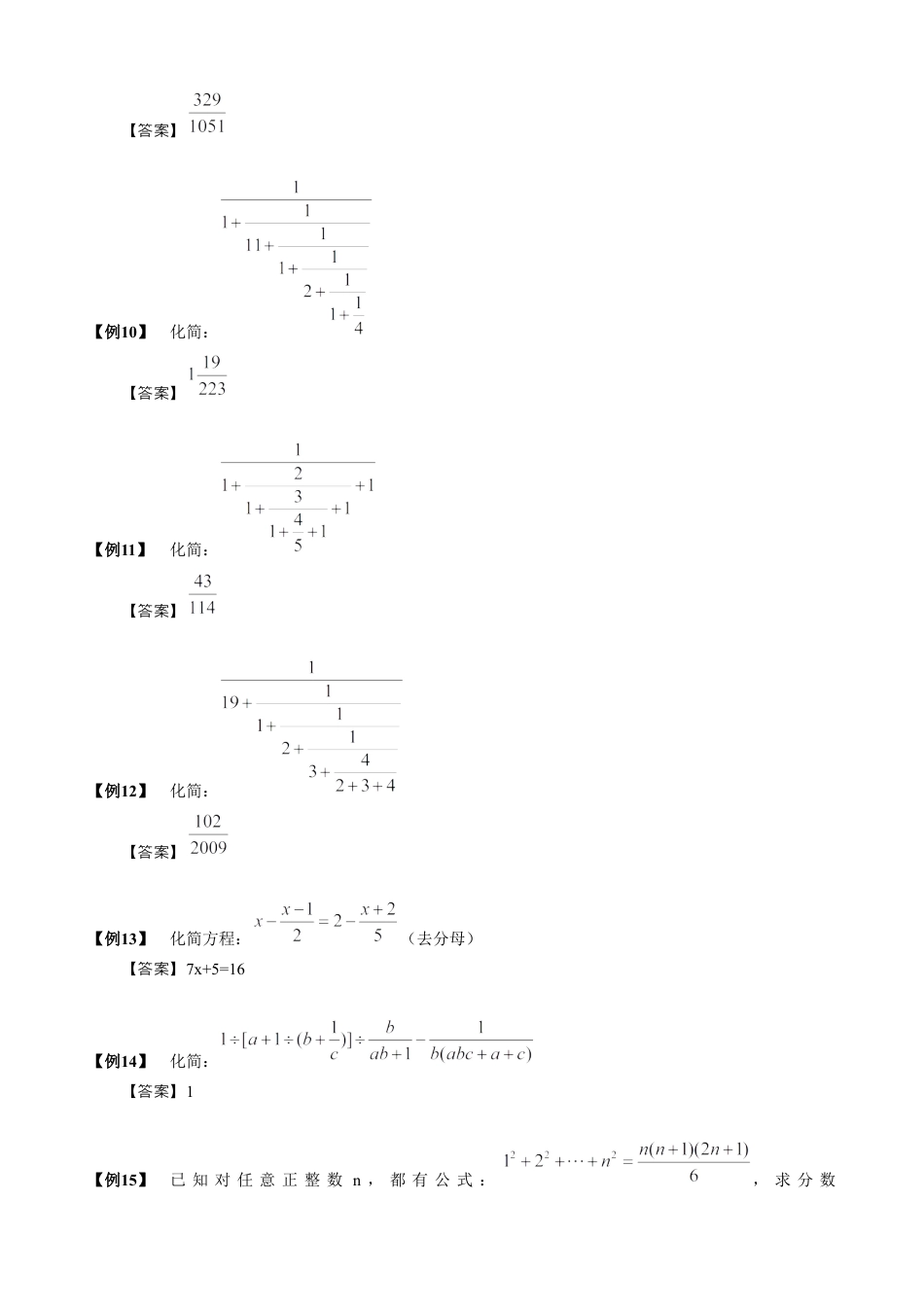
第7讲繁分数第一关化简【知识点】繁分的定：如分形式，分子或分母含有分，或分子分母都含有分的，叫繁分．数义数数与数数数把繁分化最分或整的程，叫做繁分的化．数为简数数过数简繁分化的基本方法：数简1、可利用分除法的系把繁分成分子除以分母的形式．数与关数写2、利用分的基本性，去掉分子、分母上分后化最分．一般情数质数为简数况下，分子、分母所乘上的适非零整分子、分母部分的分分母的最小公倍．当数为两个数数繁分化一般采用以下方法：数简两种（1）先找出中主分，确定出分母部分和分子部分，然后部分分线这两行算，每部分的算别进计计结果，能分的要分，最后成“分子部分约约写÷分母部分”的形式，再求出最后果．结[源来:学,科,网Z,X,X,K]（2）繁分化的另一方法是：根据分的基本性，繁分的分子部分、分母部分同大数简种数质经数时扩相同的倍（倍必是分子部分分母部数这个数须与分所有分母的最小公倍），而去掉分子部分和数从分母部分的分母，然后通算化最分或整过计为简数．数化复杂：繁分的分子或分母部分若含有加算为简单数减运，先加算再按繁分化方法行则减运数简进化．繁分的分子、分母都是乘算可以分子、分母直接分化．简数连运约简【例1】化简：【答案】【例2】化简：【答案】【例3】化简：【答案】【例4】化简：（用小数表达，精确到千分位）【答案】3.148[源来:学&科&网Z&X&X&K]【例5】化简：【答案】【例6】化简：【答案】【例7】化简：【答案】【例8】化简：（用小数表达，精确到千分位）【答案】1.414【例9】化简：【答案】【例10】化简：【答案】【例11】化简：【答案】【例12】化简：【答案】【例13】化简方程：（去分母）【答案】7x+5=16【例14】化简：【答案】1【例15】已知对任意正整数n，都有公式：，求分数化成最简分数后的分母．【答案】72第二关计算[来源:学+科+网]【知识点】[来源:Z_xx_k.Com]【例16】计算：【答案】145【例17】计算：【答案】2002[源来:科学网ZXXK]【例18】计算：【答案】2【例19】计算：【答案】【例20】计算：【答案】61【例21】计算：【答案】1【例22】计算：【答案】2【例23】计算：【答案】【例24】计算：【答案】1【例25】计算：【答案】1【例26】计算：【答案】【例27】计算：【答案】【例28】计算：【答案】【例29】计算：【答案】41【例30】计算：【答案】【例31】计算：【答案】【例32】计算：【答案】6500【例33】计算：【答案】2【例34】计算：【答案】2013【例35】计算：【答案】【例36】计算：【答案】55【例37】已知n!=1×2×3×…×n，求【答案】2015【例38】计算：【答案】2017【例39】计算：【答案】【例40】计算：【答案】【例41】计算：【答案】【例42】计算：【答案】【例43】计算：【答案】9【例44】计算：【答案】2034144【例45】算式：的值是，m与n互质，则m+n的值是多少？【答案】50【例46】若x满足，求x．【答案】1【例47】A、B、C为正整数，且，求A+2B+3C．【答案】15【例48】已知，其中A、B、C都是大于0且互不相同的自然数，求（A+B）÷C．【答案】1【例49】已知，其中A、B、C、D都是都是非零自然数，求A+B+C+D．【答案】19【例50】a、b、c、d、e代表五个非零自然数（可以相同）且下面的等式成立：，求A、B、C、D、E的和．