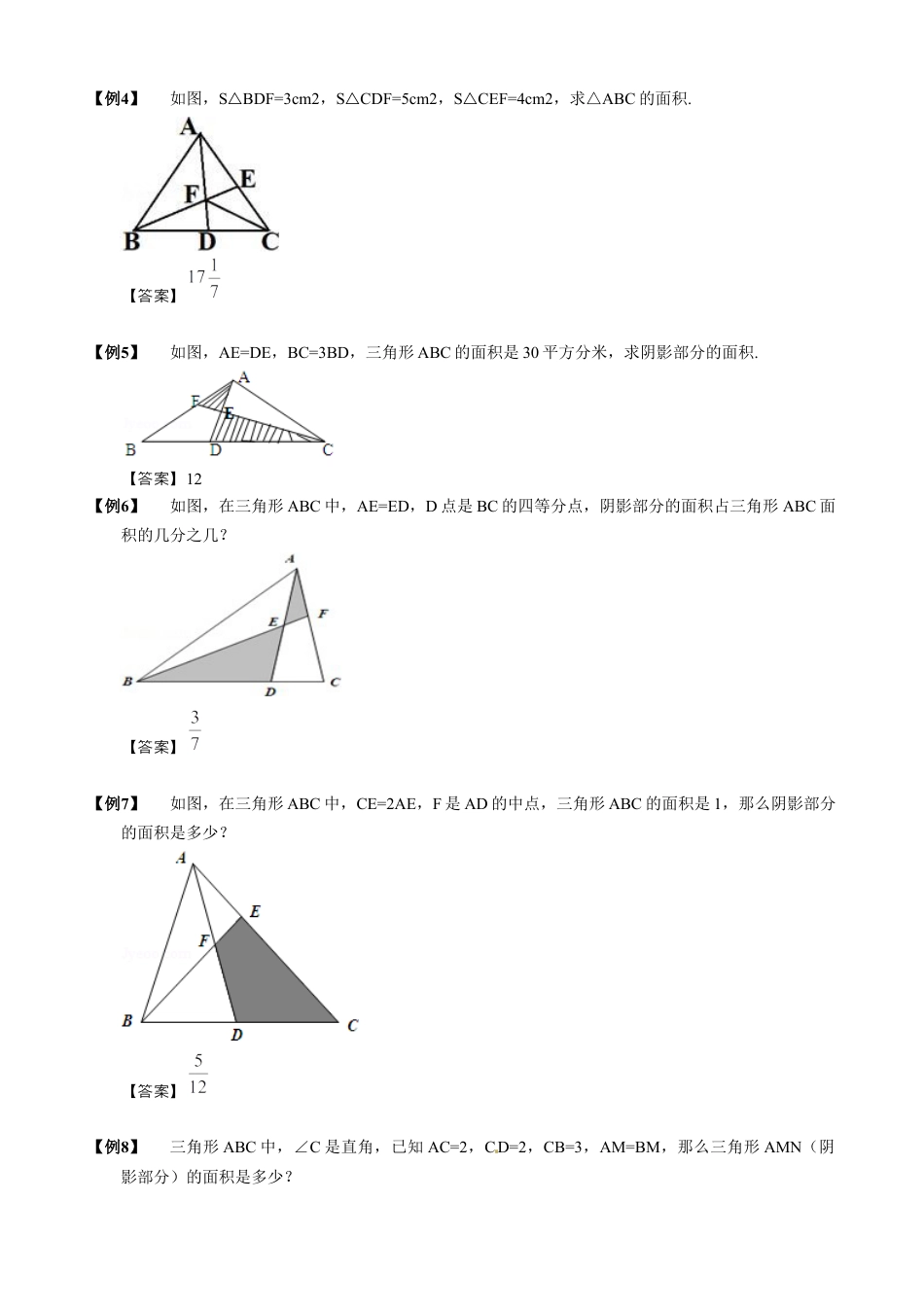
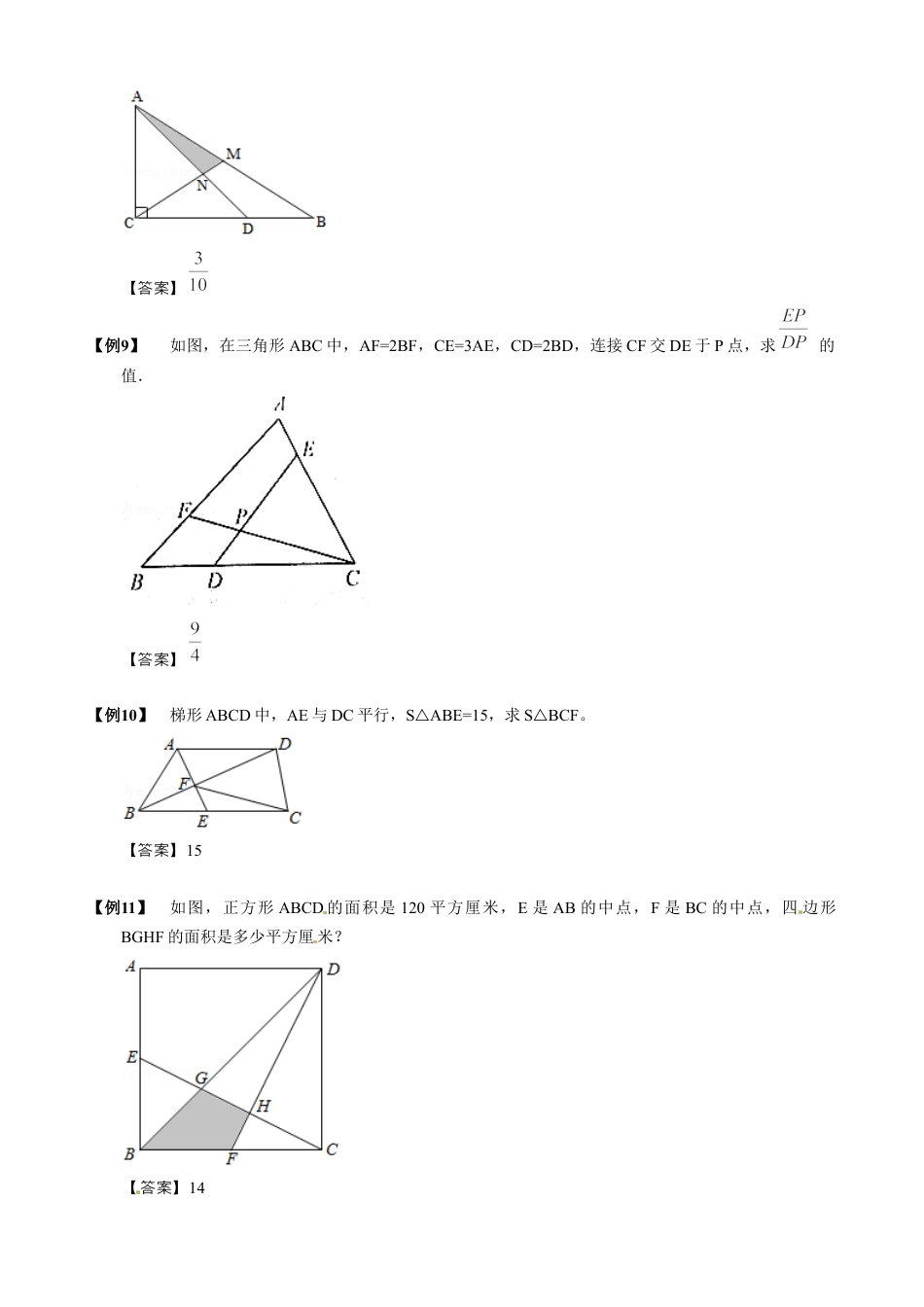
第9讲燕尾定理第一关基础燕尾定理【知识点】燕尾定理，因此似燕尾而得名，是五大模型之一，是一于三角形的定理（如△图类个关图ABC，D、E、F为BC、CA、AB上点，足满AD、BE、CF交于同一点O）．SABC△中，SAOB△：SAOC=SBDO△△：SCDO=BD△：CD；同理，SAOC△：SBOC=SAFO△△：SBFO=AF△：BF；SBOC△：SBOA=SCEO△△：SAEO=EC△：AE．【例1】对角线把梯形ABCD分﹣成四个三角形．已知两个三角形的面积分别是5和20．求梯形ABCD的面积是多少？【答案】45【例2】如图，BD：DC=2：3，AE：CE=5：3，求AF：BF。【答案】5：2【例3】如图，△ABC中，E是AD的中点，已知△ABC的面积是2，△BEF的面积是，求△AEF的面积.【答案】【例4】如图，SBDF=3cm2△，SCDF=5cm2△，SCEF=4cm2△，求△ABC的面积.[来源:学科网ZXXK]【答案】【例5】如图，AE=DE，BC=3BD，三角形ABC的面积是30平方分米，求阴影部分的面积.【答案】12[源来:学,科,网][源来:学.科.网]【例6】如图，在三角形ABC中，AE=ED，D点是BC的四等分点，阴影部分的面积占三角形ABC面积的几分之几？【答案】【例7】如图，在三角形ABC中，CE=2AE，F是AD的中点，三角形ABC的面积是1，那么阴影部分的面积是多少？【答案】【例8】三角形ABC中，∠C是直角，已知AC=2，CD=2，CB=3，AM=BM，那么三角形AMN（阴影部分）的面积是多少？【答案】[源来:科学网]【例9】如图，在三角形ABC中，AF=2BF，CE=3AE，CD=2BD，连接CF交DE于P点，求的值．【答案】【例10】梯形ABCD中，AE与DC平行，SABE=15△，求SBCF△。【答案】15【例11】如图，正方形ABCD的面积是120平方厘米，E是AB的中点，F是BC的中点，四边形BGHF的面积是多少平方厘米？【答案】14【例12】如图，BD、CF将长方形ABCD分成4块，△DEF的面积是4平方厘米，△CED的面积是6平方厘米，则四边形ABEF的面积是多少平方厘米？【答案】11【例13】如图，长方形ABCD的面积是2平方厘米，EC=2DE，F是DG的中点．阴影部分的面积是多少平方厘米？【答案】【例14】如图，在△ABC中，BD=AD，EF=3，FC=2，△ADH与△AGC的面积和等于四边形EFGH的面积，那么BE的长是多少？【答案】1[源来:Z*xx*k.Com]【例15】如图，正方形ABCD被分成了面积相同的8个三角形，如果DG=5，那么正方形ABCD面积是多少？【答案】64【例16】如图所示，正方形ABCD的面积为9平方厘米，正方形EFGH的面积为36平方厘米，边BC落在EH上．已知三角形AGC的面积为6.75平方厘米，求三角形ABE的面积．【答案】2.25