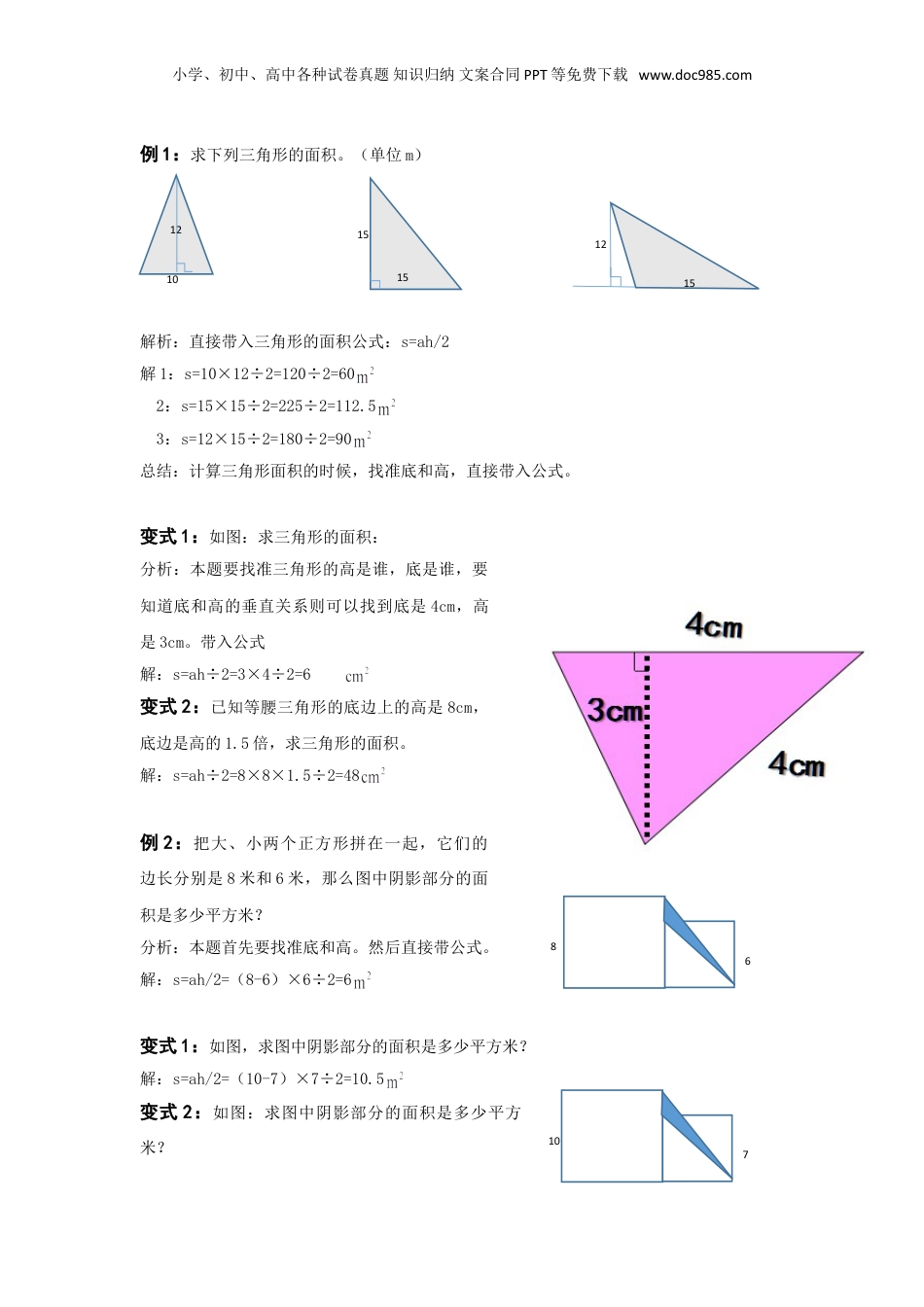
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第四-五讲平面图形的特征及计算三角形一、知识梳理由三条线段围成的图形（每相邻两条线段的端点相连）叫做三角形。（1）特征三角形都有三条边、三个顶点、三个角；三角形内角和是180度。从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段叫三角形的高，这条对边叫做三角形的底。三角形有三条高。三角形具有稳定性。（2）计算公式三角形面积：三角形面积＝底×高÷2用字母表示：s=ah/2（3）分类按角分锐角三角形：三个角都是锐角。直角三角形：有一个角是直角。等腰三角形的两个锐角各为45度，它有一条对称轴。钝角三角形：有一个角是钝角。按边分不等边三角形：三条边长度不相等。等腰三角形：有两条边长度相等；两个底角相等；有一条对称轴。等边三角形：三条边长度都相等；三个内角都是60度；有三条对称轴。二、例题精讲107小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例1：求下列三角形的面积。（单位m）解析：直接带入三角形的面积公式：s=ah/2解1：s=10×12÷2=120÷2=602：s=15×15÷2=225÷2=112.53：s=12×15÷2=180÷2=90总结：计算三角形面积的时候，找准底和高，直接带入公式。变式1：如图：求三角形的面积：分析：本题要找准三角形的高是谁，底是谁，要知道底和高的垂直关系则可以找到底是4cm，高是3cm。带入公式解：s=ah÷2=3×4÷2=6变式2：已知等腰三角形的底边上的高是8cm，底边是高的1.5倍，求三角形的面积。解：s=ah÷2=8×8×1.5÷2=48例2：把大、小两个正方形拼在一起，它们的边长分别是8米和6米，那么图中阴影部分的面积是多少平方米？分析：本题首先要找准底和高。然后直接带公式。解：s=ah/2=（8-6）×6÷2=6变式1：如图，求图中阴影部分的面积是多少平方米？解：s=ah/2=（10-7）×7÷2=10.5变式2：如图：求图中阴影部分的面积是多少平方米？12101515151286EABCD小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解：s=ah/2=6×6÷2=18例3：如图，平行四边形ABCD的面积是32平方厘米，三角形CED是一个直角三角形，已知AE=5厘米，CE=4厘米，那么阴影部分的面积是多少平方厘米？分析：可以把平行四边形分成一个矩形和2个相等的三角形，用总面积减去矩形的面积除以2即可：解：s=(32-5×4）÷2=12÷2=6（平方厘米）变式1：如上图：若四边形ABCE的面积是26平方厘米，AE=5厘米，CE=4厘米，那么阴影部分的面积是多少平方厘米？解：s=26-5×4=26-20=6（平方厘米）变式2：在上题中，已知平行四边形ABCD的面积是32平方厘米，无其余条件，则阴影三角形的面积最大是多少？解：S=32÷2=16（平方厘米）例4：如图，在平行四边形ABCD中，三角形BCE的面积是42平方厘米，BC的长度为14厘米，AE的长度为9厘米，三角形ECD的面积又是多少平方厘米？分析：知道三角形BCE的面积和BC的长度，则可以求高，AE=9，求得ED=5，则可以直接带公式。解：s=42x2÷14x(14-9）÷2=15（平方厘米）变式1：如上图，三角形ECD的面积是15平方厘米，BC的长度为14厘米，AE的长度为968ABCDE小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com厘米，三角形BCE的面积又是多少平方厘米？解：三角形的高h=14x2÷（14-9）=6cmS=14x6÷2=42（平方厘米）变式2：如上图，若有一平行四边形菜地，总面积是42平方米，共收获420kg白菜，则三角形ECD菜地大约收获多少白菜？分析：收获的菜与其面积成正比，面积越大则收获的越多。解s=42x2÷14x(14-9）÷2=15（平方米）收获白菜：420÷42x15=150kg例5：每个小方格的边长表示1CM,三角形的面积是多少?分析：由图可以看出，三角形的底边是7，高是4带入公式S=7×4÷2=14（平方厘米）变式1：如下图，每个小方格的边长表示1CM,三角形的面积是多少?小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解：s=2×3÷2=3（平方厘米）变式2：如下图，每相邻三个点所形成的三角形都是面积为1的等边三角形，计算△ABC的面积.分析这是个三角形，虽然有三角形面积公式可用，但判断它的底和高...