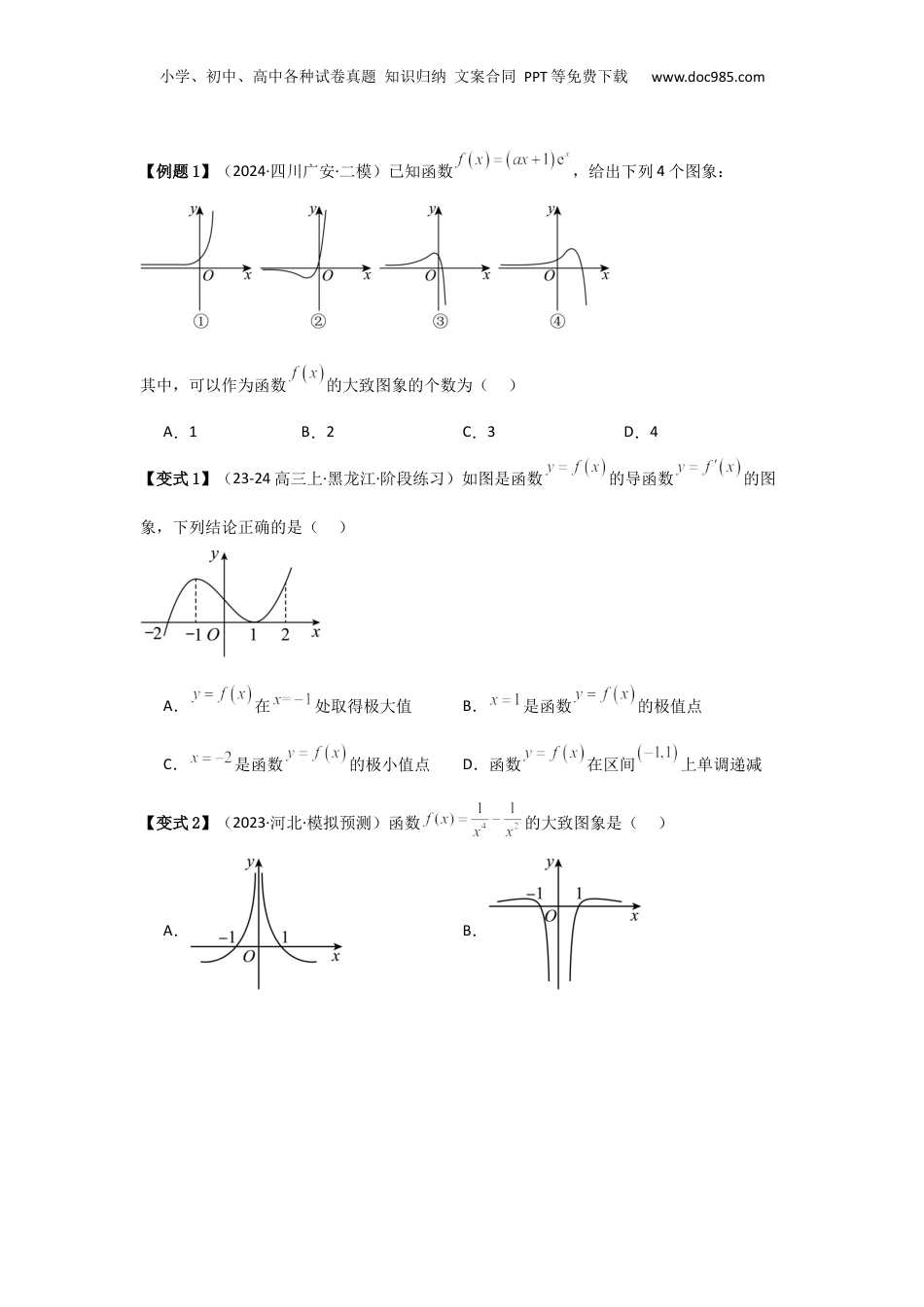
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点18导数与函数的极值、最值（2种核心题型+基础保分练+综合提升练+拓展冲刺练）【考试提醒】1.借助函数图象，了解函数在某点取得极值的必要和充分条件.2.会用导数求函数的极大值、极小值.3.掌握利用导数研究函数最值的方法.4.会用导数研究生活中的最优化问题．【知识点】1．函数的极值(1)函数的极小值函数y＝f(x)在点x＝a处的函数值f(a)比它在点x＝a附近其他点处的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧，右侧，则a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．(2)函数的极大值函数y＝f(x)在点x＝b处的函数值f(b)比它在点x＝b附近其他点处的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧，右侧，则b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．(3)极小值点、极大值点统称为，极小值和极大值统称为．2．函数的最大(小)值(1)函数f(x)在区间[a，b]上有最值的条件：如果在区间[a，b]上函数y＝f(x)的图象是一条的曲线，那么它必有最大值和最小值．(2)求函数y＝f(x)在区间[a，b]上的最大(小)值的步骤：①求函数y＝f(x)在区间(a，b)内的；②将函数y＝f(x)的各极值与比较，其中最大的一个是最大值，最小的一个是最小值．常用结论对于可导函数f(x)，“f′(x0)＝0”是“函数f(x)在x＝x0处有极值”的必要不充分条件【核心题型】题型一利用导数求解函数的极值问题根据函的数极值(点)求的要参数两个领(1)列式：根据点极值处导数为0和件列方程，利用待定系法求解；极值这两个条组数(2)：求解后根的合理性．验证验证命题点1根据函数图象判断极值小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例题1】（2024·四川广安·二模）已知函数，给出下列4个图象：其中，可以作为函数的大致图象的个数为（）A．1B．2C．3D．4【变式1】（23-24高三上·黑龙江·阶段练习）如图是函数的导函数的图象，下列结论正确的是（）A．在处取得极大值B．是函数的极值点C．是函数的极小值点D．函数在区间上单调递减【变式2】（2023·河北·模拟预测）函数的大致图象是（）A．B．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．D．【变式3】（2024高三·全国·专题练习）已知函数f（x）的导函数f′（x）的图象如图所示，则下列结论正确的是（）A．曲线y＝f（x）在点（1，f（1））处的切线斜率小于零B．函数f（x）在区间（－1，1）上单调递增C．函数f（x）在x＝1处取得极大值D．函数f（x）在区间（－3，3）内至多有两个零点命题点2求已知函数的极值【例题2】（2024·宁夏银川·一模）若函数在处取得极大值，则的极小值为（）A．B．C．D．【变式1】（2023·全国·模拟预测）函数在区间的极大值、极小值分别为（）A．，B．，C．，D．，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式2】（多选）（2024·全国·模拟预测）已知则方程可能有（）个解.A．3B．4C．5D．6【变式3】（2024·辽宁鞍山·二模）的极大值为．命题点3已知极值(点)求参数【例题3】（2024·全国·模拟预测）设为函数（其中）的两个不同的极值点，若不等式成立，则实数的取值范围为（）A．B．C．D．【变式1】（2024·四川绵阳·三模）若函数有唯一极值点，则下列关系式一定成立的是（）A．B．C．D．【变式2】（2024·辽宁·一模）已知函数在处有极值8，则等于．【变式3】（2024·全国·模拟预测）已知函数．(1)若的极值为－2，求a的值；(2)若m，n是的两个不同的零点，求证：．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型二利用导数求函数最值求含有的函的最，需先求函的定域、函，通分，判函参数数值数义导数过对参数类讨论断的性，而得到函数单调从数f(x)的最．值命题点1不含参函数的最值【例题4】（2024·陕西·模拟预测），有恒成立，则实数的取值范围为（）A．B．C．D．【变式1】（2024·四川·模拟预测）已知，若存在，使得成立，则实数的取值范围是.【变式2】（2024·上海徐汇·二模）如图，两条足...