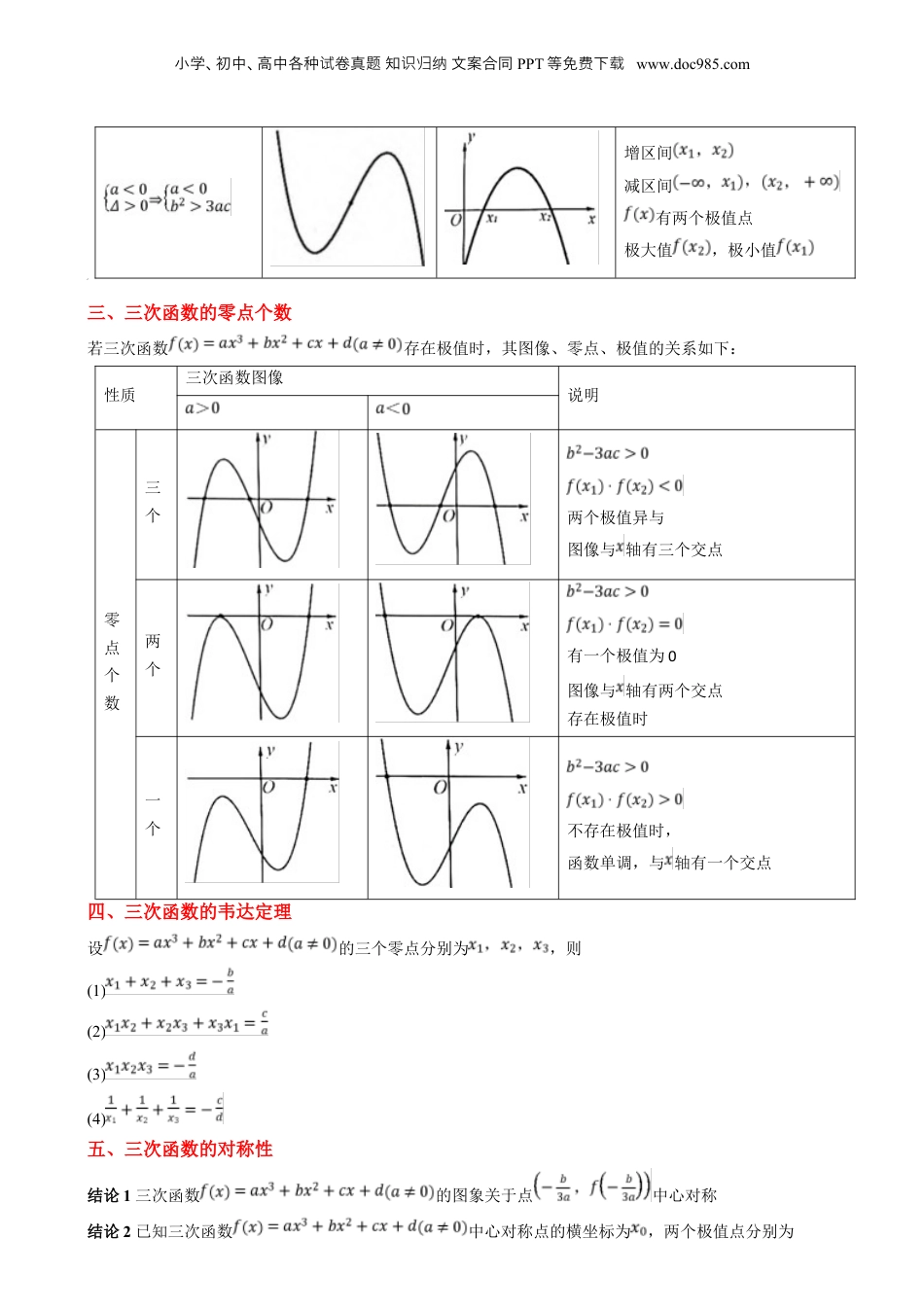
小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com2025年高考数学一轮复习讲义及高频考点归纳与方法总结（新高考通用）思维拓展06三次函数的图像与性质（精讲+精练）一、三次函数概念定义：形如叫做三次函敞，把叫做三次函数导函数的判别式当时，令，记两根为二、三次函数的图像及单调性注：三次函数要么无极值点，要么有两个，不可能只有一个！系数关系式的图像的图像的性质恒成立在上递增无极值点恒成立在上递减无极值增区间减区间有两个极值点极大值，极小值小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com增区间减区间有两个极值点极大值，极小值三、三次函数的零点个数若三次函数存在极值时，其图像、零点、极值的关系如下：性质三次函数图像说明零点个数三个两个极值异与图像与轴有三个交点两个有一个极值为0图像与轴有两个交点存在极值时一个不存在极值时，函数单调，与轴有一个交点四、三次函数的韦达定理设的三个零点分别为，则(1)(2)(3)(4)五、三次函数的对称性结论1三次函数的图象关于点中心对称结论2已知三次函数中心对称点的横坐标为，两个极值点分别为小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.com，则结论3若图像关于点对称，则图像关于轴对称点对称函数的导数是轴对称函数，轴对称函数的导数是点对称函数奇函数的导数是偶函数，偶函数的导数是奇函数，周期函数的导数还是周期函数【典例1】（多选题）（2024·全国·模拟预测）已知函数下列结论中正确的是（）A．若，则是的极值点B．，使得C．若是的极小值点，则在区间上单调递减D．函数的图象是中心对称图形【典例2】（多选题）（2024·湖北武汉·模拟预测）设函数，则下列结论正确的是（）A．存在实数使得B．方程有唯一正实数解C．方程有唯一负实数解D．有负实数解【题型训练-刷真题】一、单选题1．（2023·全国·高考真题）函数存在3个零点，则的取值范围是（）A．B．C．D．二、多选题2．（2024·全国·高考真题）设函数，则（）A．是的极小值点B．当时，C．当时，D．当时，3．（2024·全国·高考真题）设函数，则（）A．当时，有三个零点B．当时，是的极大值点C．存在a，b，使得为曲线的对称轴小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.comD．存在a，使得点为曲线的对称中心4．（2022·全国·高考真题）已知函数，则（）A．有两个极值点B．有三个零点C．点是曲线的对称中心D．直线是曲线的切线三、填空题5．（2024·全国·高考真题）曲线与在上有两个不同的交点，则的取值范围为．【题型训练-刷模拟】一、单选题1．（2023·广西·模拟预测）设，若为函数的极大值点，则（）A．B．C．D．2．（2023·辽宁葫芦岛·二模）已知函数，则（）A．有一个极值点B．有两个零点C．点（0，1）是曲线的对称中心D．直线是曲线的切线3．（23-24高三上·上海普陀·期中）已知函数，则以下正确的个数有（）（1）有两个极值点；（2）的驻点为和；（3）有3个零点；（4）直线是曲线的切线.A．0个B．1个C．2个D．3个4．（23-24高三上·云南·阶段练习）关于函数，则下列说法正确的是（）A．函数在上单调递减B．当时，函数在上恒成立C．当或时，函数有2个零点D．当时，函数有3个零点，记为，则5．（23-24高二下·广东广州·期中）已知函数的导函数的极值点同时也是的零点，则（）A．小学、初中、高中各种卷真知文案合同试题识归纳PPT等免下费载www.doc985.comB．在R上单调递增C．的图象关于点中心对称D．过坐标原点只有两条直线与曲线相切二、多选题6．（23-24高二下·重庆·阶段练习）定义：设是的导函数，是函数的导数，若方程有实数解，则称点为函数的“拐点”.经过探究发现：任何一个三次函数都有“拐点”且“拐点”就是三次函数图象的对称中心.已知函数图象的对称中心为，则下列说法中正确的有（）A．，B．函数的极大值与极小值之和为6C．函数有三个零点D．函数在区间上的最小值为17．（23-24高三下·重庆沙坪坝·阶段练习）已知三次函数有三个不同的零点，函数.则（）A．B．若成等差数列，则C．若恰有两个不同的零点...