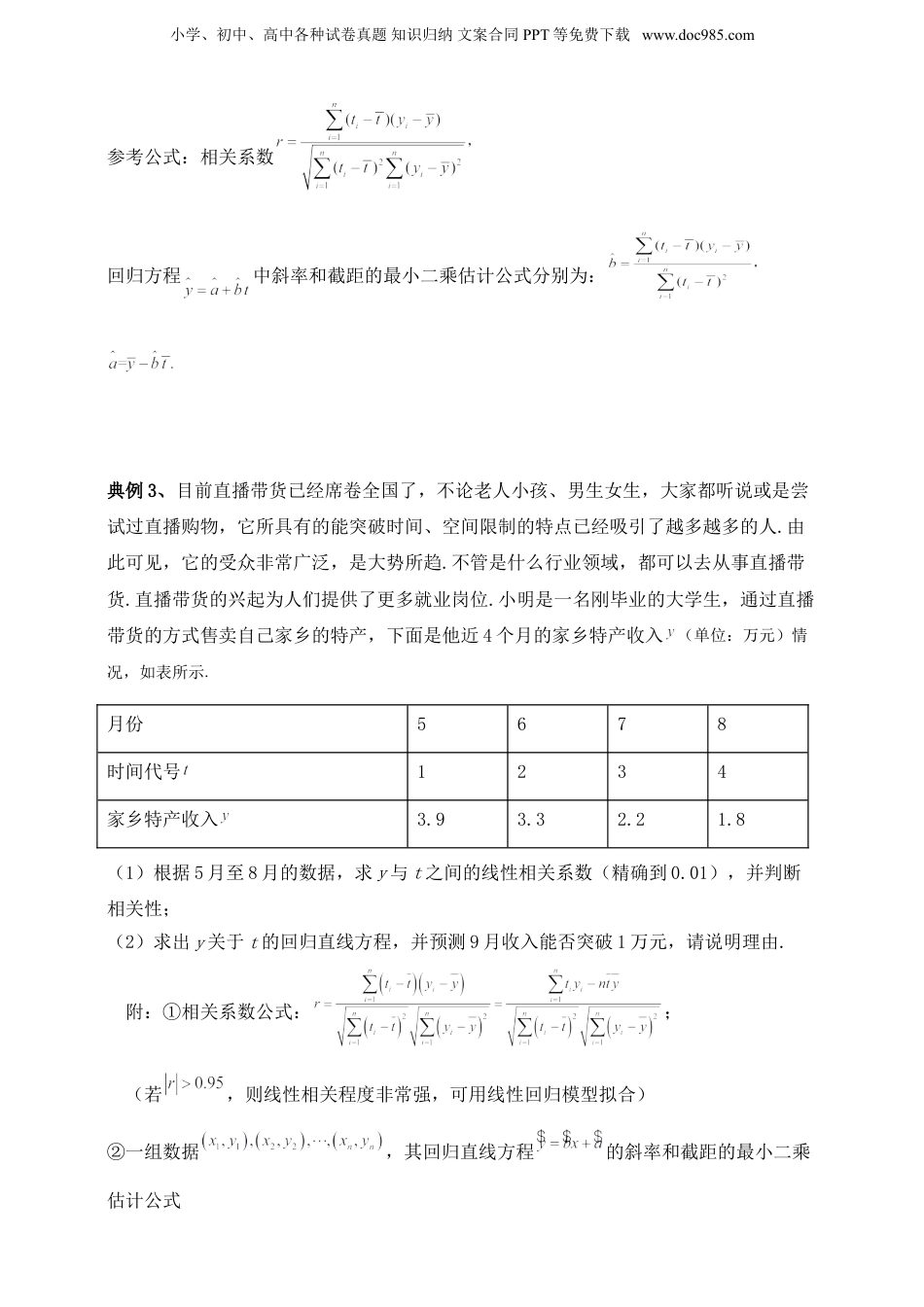
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com人教A版数学--概率专题九知识点一求回归直线方程,相关系数的意义及辨析,相关系数的计算,根据回归方程进行数据估计典例1、某产品的广告费用支出与销售额之间有如下的对应数据：245683040605070（1）求回归直线方程；（2）据此估计广告费用为10时销售收入的值.附：线性回归方程中系数计算公式，，其中，表示样本均值.随堂练习：某景区对2018年1-5月的游客量x与利润y的统计数据如表：月份12345游客量（万人）46578利润（万元）1934264145（1）根据所给统计数据，求y关于x的线性回归方程；（2）据估计6月份将有10万游客光临，请你判断景区上半年的总利润能否突破220万元？（参考数据：，），．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例2、为打造“四态融合、产村一体”的望山、见水、忆乡愁的美丽乡村，增加农民收入，某乡政府在近几年中任选了5年，经统计，年份代号x与景区农家乐接待游客人数y（单位：万人）的数据如下表：年份代号x23578接待游客人数y（万人）33.546.58（1）根据数据说明变量x与y是正相关还是负相关；（2）求相关系数r的值，并说明年份与接待游客数的相关性的强与弱；（3）分析近几年中该景区农家乐接待游客人数y的变化情况，求该景区农家乐接待游客人数关于年份代号的回归直线方程；并预测在年份代号为10时该景区农家乐接待游客的人数（单位：万人，精确到小数点后2位）.附：一般地，当r的绝对值大于0.75时认为两个变量之间有很强的线性关系.,.随堂练习：下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.（1）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；（2）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.附注：参考数据：，，，≈2.646.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com参考公式：相关系数回归方程中斜率和截距的最小二乘估计公式分别为：典例3、目前直播带货已经席卷全国了，不论老人小孩、男生女生，大家都听说或是尝试过直播购物，它所具有的能突破时间、空间限制的特点已经吸引了越多越多的人.由此可见，它的受众非常广泛，是大势所趋.不管是什么行业领域，都可以去从事直播带货.直播带货的兴起为人们提供了更多就业岗位.小明是一名刚毕业的大学生，通过直播带货的方式售卖自己家乡的特产，下面是他近4个月的家乡特产收入（单位：万元）情况，如表所示.月份5678时间代号1234家乡特产收入3.93.32.21.8（1）根据5月至8月的数据，求y与t之间的线性相关系数（精确到0.01），并判断相关性；（2）求出y关于t的回归直线方程，并预测9月收入能否突破1万元，请说明理由.附：①相关系数公式：；（若，则线性相关程度非常强，可用线性回归模型拟合）②一组数据，其回归直线方程的斜率和截距的最小二乘估计公式小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com分别为，；③参考数据：，，.随堂练习：某公司为确定下一年度投入某种产品的研发费，需了解年研发费x（单位：万元）对年销售量y（单位：百件）和年利润（单位：万元）的影响，现对近6年的年研发费和年销售量（，2，…，6）数据作了初步处理，得到下面的散点图及一些统计量的值.12.52223.5157.54.51854270小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com表中，.（1）根据散点图判断与哪一个更适宜作为年研发费x的回归方程类型；（给出判断即可，不必说明理由）（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；（3）已知这种产品的年利润，根据（2）的结果，当年研发费为多少时，年利润z的预报值最大？附：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为，.知识点独立事件的乘法公式,独立重复试验的概率问题,求离散型随机变量的均值典例4、甲乙两人轮流投篮，每人每次投一球､.甲先投且先投中者获胜，约定有人获胜或每人都已投球2次时投篮结束.设甲每次投篮投中的概率为，乙每次投篮...