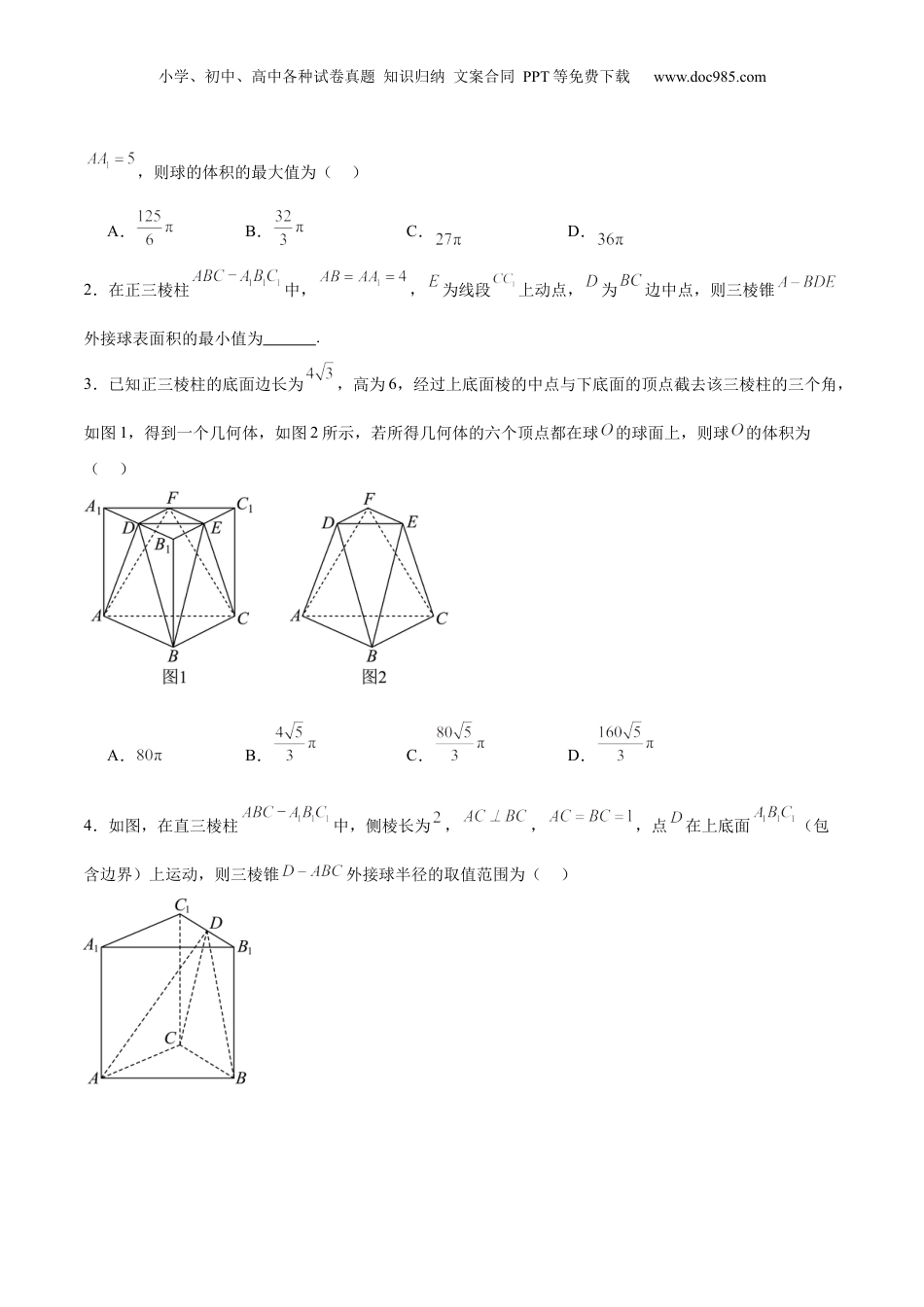
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com特训09多面体与求内切外接问题（八大题型）一、外接球问题若一个简单多面体的所有顶点都在一个球面上，则该球为此多面体的外接球。简单多面体的外接球问题是立体几何的重点和难点，此类问题实质是解决球的半径长或确定球心位置问题，其中球心位置的确定是关键，下面介绍几种常见的球心位置的确定方法。如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心。由此，可以得到确定简单多面体外接球的球心位置有如下结论：结论1：正方体或长方体的外接球的球心为其体对角线的中点。结论2：正棱柱的外接球的球心是上、下底面中心连线的中点。结论3：直棱柱的外接球的球心是上、下底面多边形外心连线的中点。结论4：正棱锥外接球的球心在其高上，具体位置通过构造直角三角形计算得到。结论5：若棱锥的顶点可构共斜边的直角三角形，则公共斜边的中点就是其外接球的球心。二、内切球问题若一个多面体的各个面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球。因此，多面体内切球球心到该多面体各个面的距离相等。并非所有多面体都有内切球，下面介绍几种常见多面体内切球问题：1.正多面体内切球的球心与其外接球的球心重合，内切球的半径为球心到多面体任一面的距离。2.正棱锥的内切球与外接球的球心都在其高线上，但不一定重合。目录：01：三棱柱02：四棱锥03：棱台04：侧棱垂直于底面05：正方体、长方体06：其他多面体07：三棱锥08：折叠问题01：三棱柱1．在一个封闭的直三棱柱内有一个体积为V的球，若，，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，则球的体积的最大值为（）A．B．C．D．2．在正三棱柱中，，为线段上动点，为边中点，则三棱锥外接球表面积的最小值为.3．已知正三棱柱的底面边长为，高为6，经过上底面棱的中点与下底面的顶点截去该三棱柱的三个角，如图1，得到一个几何体，如图2所示，若所得几何体的六个顶点都在球的球面上，则球的体积为（）A．B．C．D．4．如图，在直三棱柱中，侧棱长为，，，点在上底面（包含边界）上运动，则三棱锥外接球半径的取值范围为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．02：四棱锥5．四棱锥中，平面平面，底面为矩形，，，，若四棱锥的外接球表面积为，则四棱锥的体积为（）A．B．C．或D．或6．已知正四棱锥的侧棱长为，且二面角的正切值为，则它的外接球表面积为（）A．B．C．D．03：棱台7．已知正四棱台，半球的球心在底面的中心，且半球与该棱台的各棱均相切，则半球的表面积为（）A．B．C．D．8．在正三棱台中，，，二面角的正弦值为，则的外接球体积为（）A．B．C．D．04：侧棱垂直于底面9．如图，四棱锥中，面，四边形为正方形，，与平面所成角的大小为，且，则四棱锥的外接球表面积为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．26πB．28πC．34πD．14π10．如图，在四面体中，与均是边长为的等边三角形，二面角的大小为，则四面体的外接球表面积为.05：正方体、长方体11．已知正方体的棱长为4，点是棱的中点，为四边形内（包括边界）的一动点，且满足平面，的轨迹把正方体截成两部分，则较小部分的外接球的体积为（）A．B．C．D．12．已知一个长方体的封闭盒子，从同一顶点出发的三条棱长分别为3，4，5，盒内有一个半径为1的小球，若将盒子随意翻动，则小球达不到的空间的体积是（）A．B．C．D．06：其他多面体小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com13．如图1，一圆形纸片的圆心为，半径为，以为中心作正六边形，以正六边形的各边为底边作等腰三角形，使其顶角的顶点恰好落在圆上，现沿等腰三角形的腰和中位线裁剪，裁剪后的图形如图2所示，将该图形以正六边形的边为折痕将等腰梯形折起，使得相邻的腰重合得到正六棱台．若该正六棱台的高为，则其外接球的表面积为（）A．B．C．D．14．六氟化硫，化...