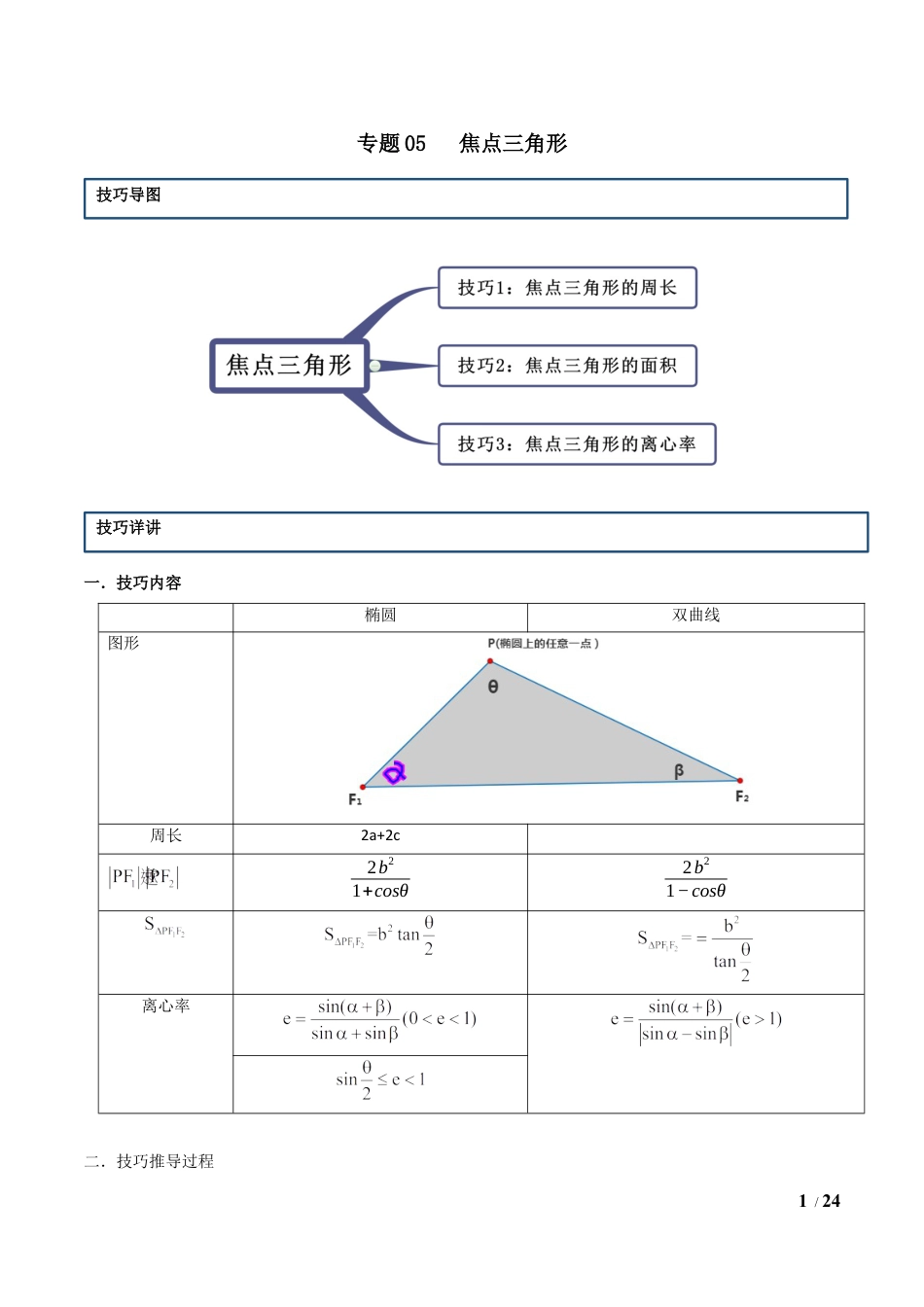
1/24专题05焦点三角形一．技巧内容二．技巧推导过程技巧导图技巧详讲椭圆双曲线图形周长2a+2c2b21+cosθ2b21−cosθ离心率2/241.2.椭圆中焦点三角形的面积公式3.椭圆中的离心率4.3/245.双曲线中焦点三角形的面积公式6.双曲线中的离心率技巧1焦点三角形的周长【例1】（2020·黑龙江）已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于（）A．20B．16C．18D．14【答案】C【解析】根据椭圆方程可知，根据椭圆的定义可知，的周长为，故选C.【举一反三】1．（2020·西藏南木林县第一中学高三月考）若椭圆（其中a＞b＞0）的离心率为，两焦点分别为F1，F2，M为椭圆上一点，且△F1F2M的周长为16，则椭圆C的方程为（）例题举证4/24A．B．C．D．【答案】D【解析】椭圆（其中a＞b＞0）的两焦点分别为F1，F2，M为椭圆上一点，且△F1F2M的周长为16，可得2a+2c=16，椭圆（其中a＞b＞0）的离心率为，可得，解得a=5，c=3，则b=4，所以椭圆C的方程为：．故选D．2．（2019·广西南宁）定义：椭圆上一点与两焦点构成的三角形为椭圆的焦点三角形，已知椭圆的焦距为，焦点三角形的周长为，则椭圆的方程是__________．【答案】【解析】设椭圆的半焦距为，由题意得，，所以，故椭圆的方程是.技巧2焦点三角形的面积【例2-1】（2020·安徽省定远中学）已知椭圆的左、右焦点分别为、，为椭圆上一点，且，若的面积为9，则__________．【答案】35/24【解析】（技巧法）（常规法）因为的面积为9，所以因为，所以即故答案为：3【例2-2】（2020·山西大同）已知、为双曲线的左、右焦点，点P在C上，，则的面积为【答案】【解析】（技巧法）（常规法）双曲线，则，所以，则，平方得，且，由余弦定理，即，解得，则.【举一反三】1．（2020·云南陆良）已知、为双曲线C：的左、右焦点，点P在C上，∠P=6/24，则（）A．2B．4C．6D．8【答案】B【解析】（技巧法）（常规法）由双曲线的定义得①,又,由余弦定理②，由①2-②得，故选B．2（2020·广东汕头）若椭圆上一点P与椭圆的两个焦点、的连线互相垂直，则的面积为()A．36B．16C．20D．24【答案】B【解析】（常规法）设则,即,又,故选B.3．（2020·上海普陀·高三三模）设为双曲线（）的上一点，，（为左、右焦点），则的面积等于（）A．B．C．D．【答案】C7/24【解析】（技巧法）（常规法）双曲线，则不妨设是双曲线的右支上一点，则由双曲线的定义，得则,所以所以，即所以所以故选：C技巧3焦点三角形的离心率【例3-1】设椭圆的左、右焦点分别为,是上的点,,,则的离心率为()8/24A.B.C.D.【答案】D【解析】(技巧法）e=sin(90°+30°)sin90°+sin30°=√33，选D。（常规法）设|PF2|=t，|PF1|=2t，则|F1F2|=√3t，即2a=3t，2c=√3t，e=2c2a=√33，选D。【例3-2】（2020·河北衡水中学）已知分别是椭圆的左、右焦点，若椭圆上存在点，使，则椭圆的离心率的取值范围为（）A．B．C．D．【答案】B【解析】（常规法））由椭圆上存在点，使可得以原点为圆心，以c为半径的圆与椭圆有公共点，∴，∴，∴∴．由，∴，即椭圆离心率的取值范围为．选B．【举一反三】1．（2020·沙坪坝·重庆一中高三月考（理））已知点P在以为左，右焦点的椭圆9/24上，在中，若，，则（）A．B．C．D．【答案】B【解析】2．（2020·安徽合肥·高三二模（文））记，为椭圆的两个焦点，若上存在点满足，则实数取值范围是()A．B．C．D．【答案】A【解析】（常规法）当焦点在x轴上时，a2＝m，b2＝1，m＞1，由对称性可知当M为上下顶点时，∠F1MF2最大，10/24因为，∴∠F1MF2，∠F1MO，所以tan∠F1MO1，即1，解得m≥2；当焦点在y轴上时，a2＝1，b2＝m，0＜m＜1，当M为左右顶点时，∠F1MF2最大，因为，∠F1MF2，∠F1MO，所以tan∠F1MO1，即1，解得0＜m，故选：A．1．（2020·全国高三单元测试）已知F1，F2是椭圆＋＝1的两焦点，过点F2的直线交椭圆于A，B两点．在△AF1B中，若有两边之和是10，则第三边的长度为()A．6B．5C．4D．3【答案】A【解析】技巧法：△AF1B的周长公式4a=16,第三边等于16-10=6技巧强化11/24常规法：因为根据已知条件可知，椭圆＋＝1中16>9,说明焦点在x轴上，同时a=4,b=3,而过点F2的直...