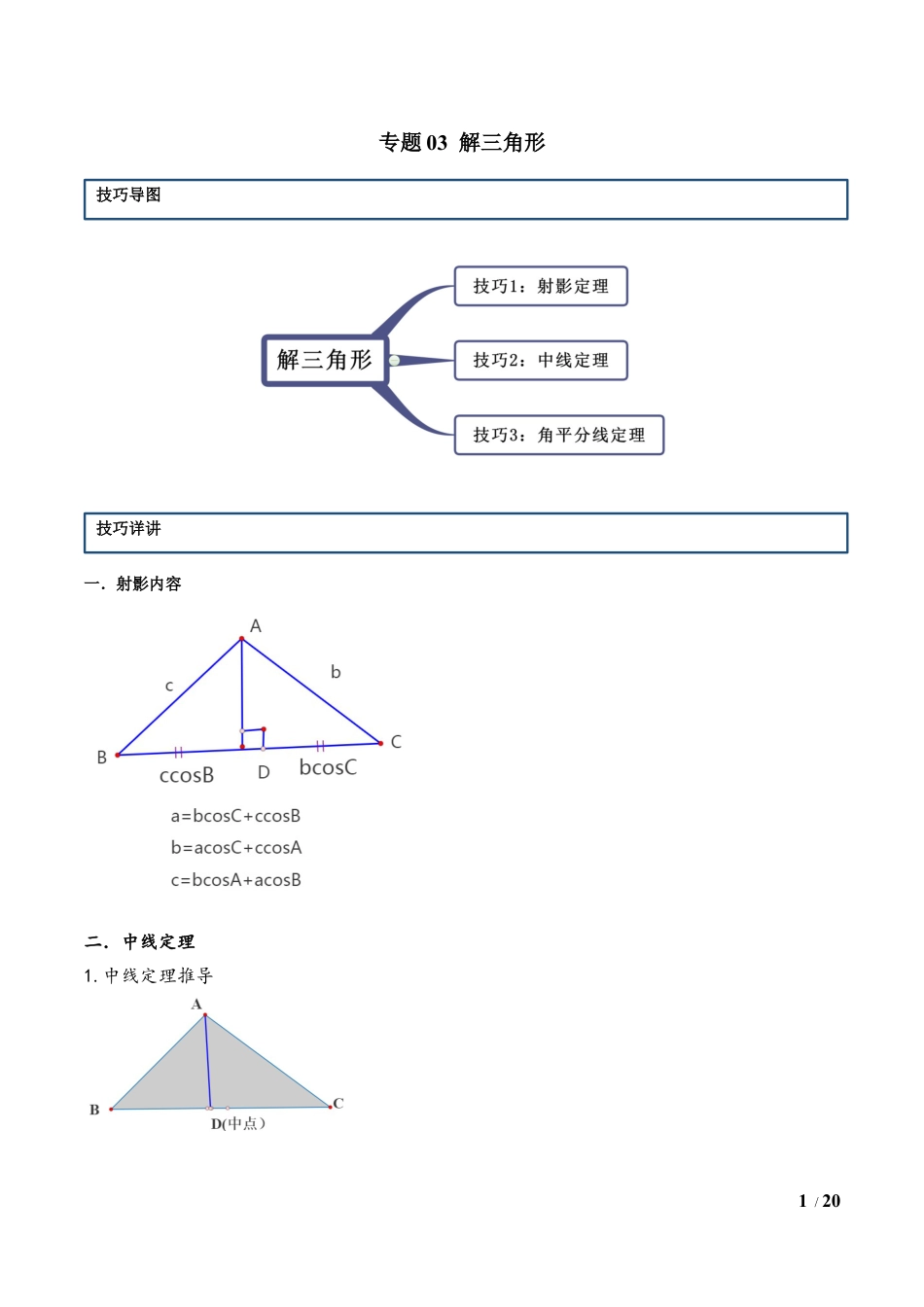
1/20专题03解三角形一．射影内容二．中线定理1.中线定理推导技巧导图技巧详讲2/202.三角形面积3.三角形的周长三．角平分线定理1.角平分线上的点到两边的距离相等2.三角形的一个角的角平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例即3/20技巧一三角形的射影定理【例1】（2017•新课标Ⅱ）的内角，，的对边分别为，，，若，则．【答案】【解析】技巧法：由射影定理可得，，，故答案为：常规法：，由正弦定理可得，，，，，，故答案为：【举一反三】1.（2020•青岛模拟）在中，内角，，所对的边分别是，，，若，且，则B=【答案】技巧举证4/20【解析】技巧法：由射影定理可得，因为，则．常规法：因为，由正弦定理可得，，因为，所以，所以，因为，则．2（2020•安徽模拟）在中，角，，的对边分别为，，．若，，，则的面积为。【答案】【解析】技巧法：由射影定理可得，，得．，解得．则的面积．常规法：，，，即，，解得，，解得．5/20，解得．则的面积．3（2020•南充模拟）的内角，，的对边分别为，，，若，则内角C=。【答案】【解析】技巧法：由射影定理可得故，又，所以．常规法：由正弦定理得：，即，即，由于，故，又，所以．技巧2三角形的中线定理【例2】（2020·梅河口市第五中学高三（理））在中，，已知边上的中线，则面积的最大值为__________．【答案】.【解析】技巧法：常规法：在△ABC中，，BC边上的中线AD=3，，设AB＝c，AC＝b，6/20平方可得9＝.化简可得，，∴bc≤36，当且仅当时成立，故△ABC的面积S＝故答案为【举一反三】1．（2020·广东高三月考（理））在中，，已知BC边上的中线，则面积的最大值为______.【答案】【解析】技巧法：常规法：中，，边上的中线长为3，，设，，平方可得：，化简可得，，可得：，故的面积．7/20故答案为：．2．（2020·全国）在锐角三角形中，角、、的对边分别为、、，向量，，且.（1）求角；（2）若，且的面积为，求边上的中线的大小.【答案】（1）；（2）.【解析】（1）因为，，，所以，由正弦定理得.因为，所以，所以，因为，所以；（2）因为的面积为，所以，因为，，所以.在中，为的中点，，由余弦定理得.所以.8/20技巧3角平分线的定理【例3】（2020·梅河口市第五中学）已知中，．是的角平分线，交于．（Ⅰ）求的值；（Ⅱ）求的长．【答案】（I）；（II）.【解析】（Ⅰ）在中，，在中，因为是的角平分线，所以（Ⅱ）法一：由题知，所以，所以法二：所以【举一反三】9/201．（2019·江苏）在中，，，角A的角平分线，则______.【答案】【解析】由题意，，，角的角平分线，在中，由正弦定理：，可得，则，所以，那么，则，所以．在中，由正弦定理：，所以.可得．故答案为：.2．（2020·梅河口市第五中学高一期末（文））已知中，是的角平分线，交于.10/20（1）求的值；（2）若，求.【答案】（1）；（2）.【解析】（1）在中，，在中，，因为是的角平分线，所以.（2）设，则，所以，所以，所以.3．（2019·河南高考模拟（理））在中，，，为的内角平分线，.（Ⅰ）求的值（Ⅱ）求角的大小【答案】（Ⅰ）2；（Ⅱ）.【解析】（Ⅰ）在三角形ABD中,由正弦定理得：11/20在三角形ACD中,由正弦定理得：因为（Ⅱ）在三角形ABD中,由余弦定理得在三角形ACD中,由余弦定理得又解得又1.（2020春•上饶月考）在中，角，，的对边分别是，，，且面积为，若，，则角等于【答案】【解析】技巧法：由射影定理可得所以，故，，，，故，则角．技巧强化12/20常规法：因为，由正弦定理可得，，即，因为，所以，故，，，，故，则角．2.（2020春•路南区校级月考）在中，内角，，所对的边分别为，，，且．若，的面积为，则b+c=【答案】4【解析】技巧法：由射影定理可得所以即，所以，，所以，因为，由余弦定理可得，，故．常规法：因为．由正弦定理可得，．因为，所以即，所以，，所以，因为，由余弦定理可得，，故．3．（2019·福建高三（理））已知为等腰三角形，，边上的中线的长为7，则的面积为__________．【答案】13/20【解析】【分析】先设等腰三角形的腰长为，进而可得底边的长，再由余弦定理列出方程，即可求出，从而可得结果.【...