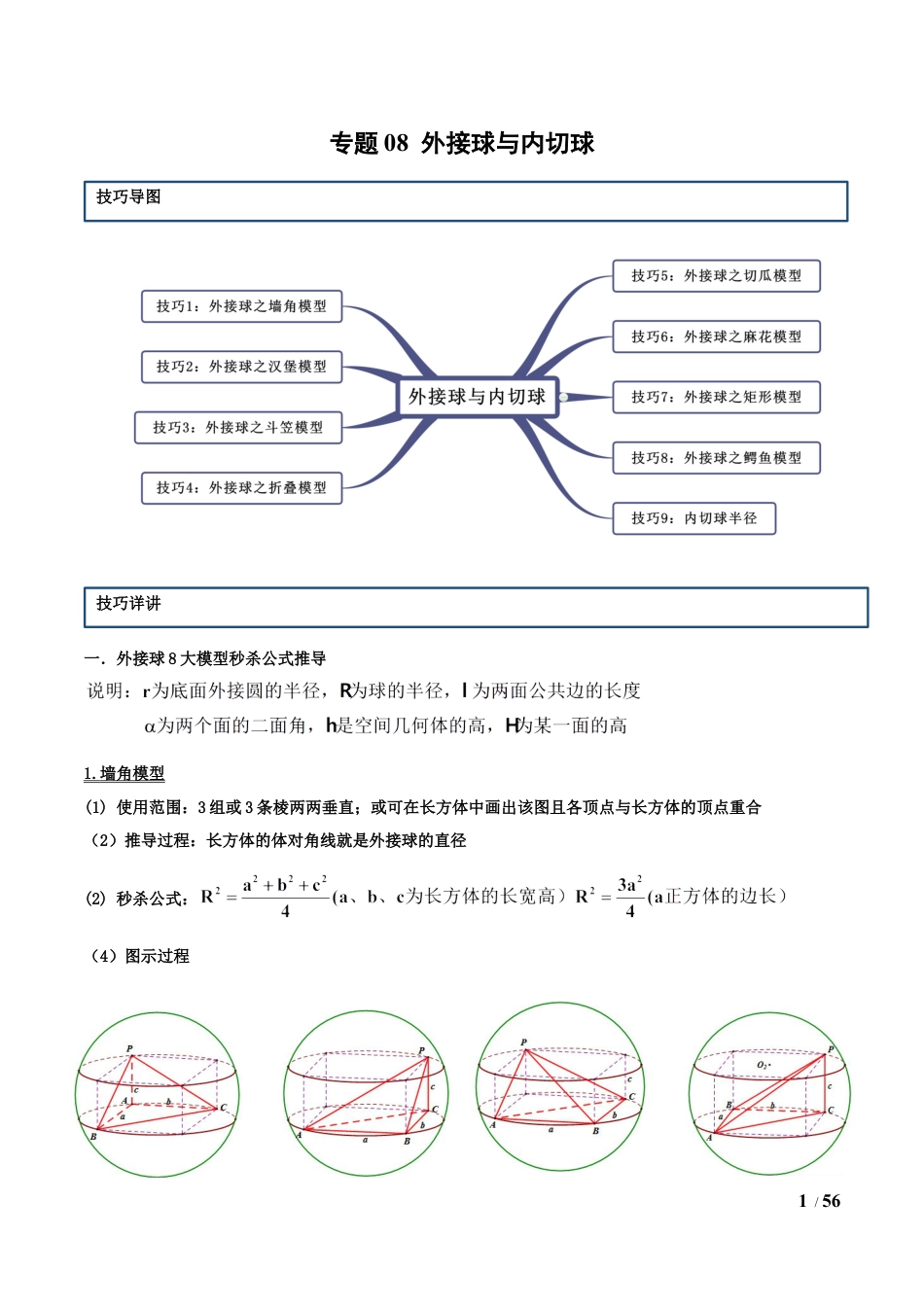
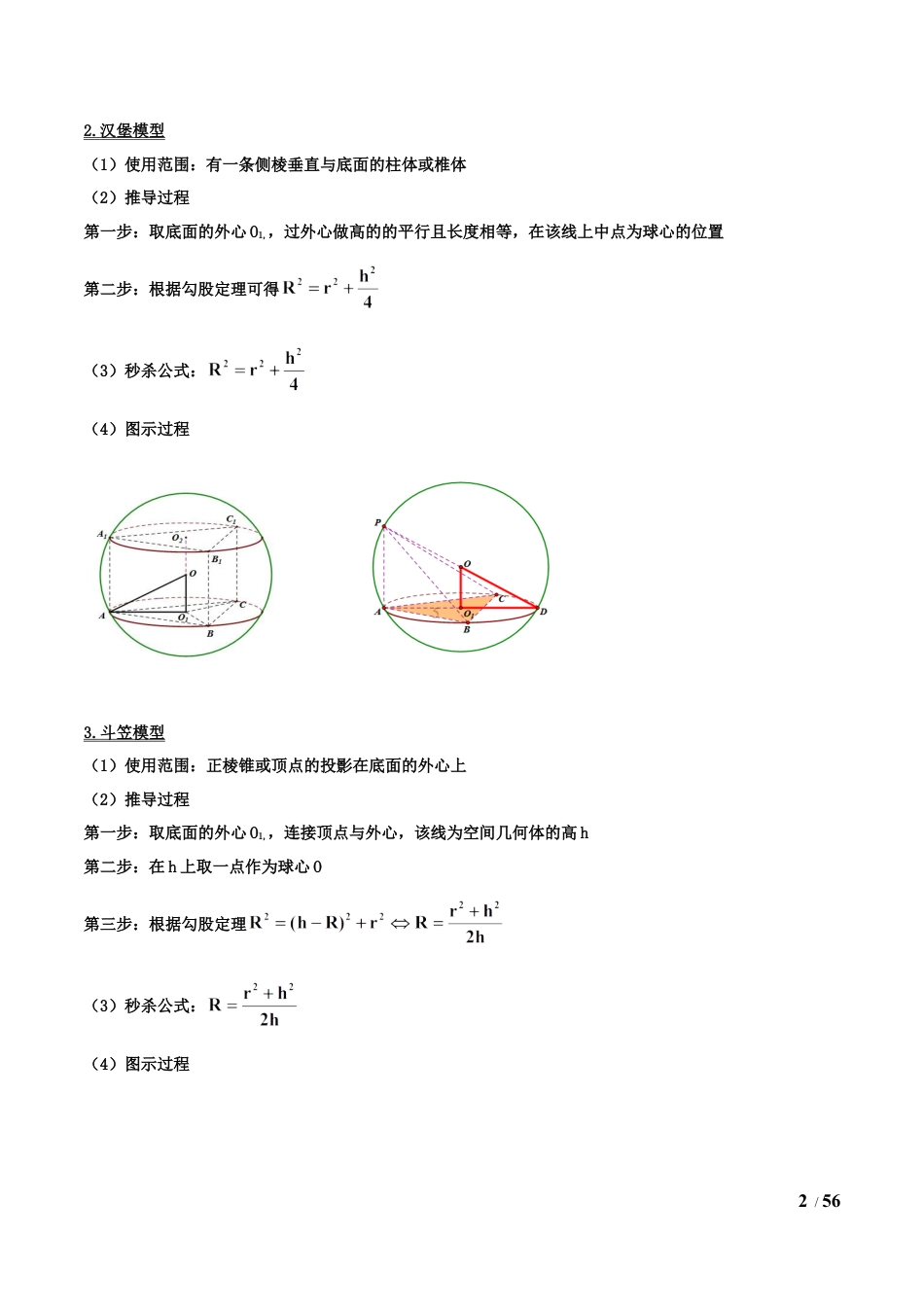
1/56专题08外接球与内切球一．外接球8大模型秒杀公式推导1.墙角模型(1)使用范围：3组或3条棱两两垂直；或可在长方体中画出该图且各顶点与长方体的顶点重合（2）推导过程：长方体的体对角线就是外接球的直径(2)秒杀公式：（4）图示过程(3)秒杀公式：技巧导图技巧详讲2/562.汉堡模型（1）使用范围：有一条侧棱垂直与底面的柱体或椎体（2）推导过程第一步：取底面的外心O1,，过外心做高的的平行且长度相等，在该线上中点为球心的位置第二步：根据勾股定理可得（3）秒杀公式：（4）图示过程3.斗笠模型（1）使用范围：正棱锥或顶点的投影在底面的外心上（2）推导过程第一步：取底面的外心O1,，连接顶点与外心，该线为空间几何体的高h第二步：在h上取一点作为球心O第三步：根据勾股定理（3）秒杀公式：（4）图示过程3/564.折叠模型（1）使用范围：两个全等三角形或等腰三角形拼在一起，或菱形折叠（2）推导过程第一步：过两个平面取其外心H1、H2，分别过两个外心做这两个面的垂线且垂线相交于球心O第二步：计算第三步：（3）秒杀技巧：（4）图示过程5.切瓜模型（1）使用范围：有两个平面互相垂直的棱锥（2）推导过程：第一步：分别在两个互相垂直的平面上取外心F、N，过两个外心做两个垂面的垂线，两条垂线的交点即为4/56球心O，取BC的中点为M，连接FM、MN、OF、ON第二步：（3）秒杀公式：（4）图示过程6.麻花模型（1）使用范围：对棱相等的三棱锥（2）推导过程：设3组对棱的长度分别为x、y、z,长方体的长宽高分别为a、b、c（3）秒杀公式：（4）图示过程5/567.矩形模型（1）使用范围：棱锥有两个平面为直角三角形且斜边为同一边（2）推导过程：根据球的定义可知一个点到各个顶点的距离相等该点为球心可得，斜边为球的直径（3）秒杀公式：（4）图示过程8.鳄鱼模型（1）使用范围：适用所有的棱锥（2）推导过程：6/56（3）秒杀公式：（4）图示过程7/56二．内切球的半径---等体积法1.推导过程2.秒杀公式：3.图示过程特别说明：下面例题或练习都是常规方法解题，大家可以利用模型的秒杀公式技巧1外接球之墙角模型【例1】（2020·河南高三月考）已知长方体中，，，与平面所成角的正弦值为，则该长方体的外接球的表面积为（）例题举证8/56A．B．C．D．【答案】B【解析】作，垂足为，连接，.因为平面平面，平面平面，平面，所以平面，所以是与平面所成的平面角.又，.所以，解得.故该长方体的体对角线为.设长方体的外接球的半径为，则，解得.所以该长方体的外接球的表面积为.故选B.9/56【举一反三】1．（2020·全国高三专题练习）棱长为的正方体的外接球的表面积为（）A．B．C．D．【答案】C【解析】因为正方体的外接球的直径为正方体的体对角线的长，所以，解得，所以球的表面积为：.故选：C2．（2019·绥德中学）球面上有四个点，若两两垂直，且，则该球的表面积为（）A．B．C．D．【答案】D【解析】由题意可知，该球是一个棱长为4的正方体的外接球，设球的半径为，由题意可得：,据此可得：，外接球的表面积为：.本题选择D选项.技巧2外接球之汉堡模型【例2】（2020·四川泸州市·高三）已知四棱锥中，四边形是边长为2的正方形，且平面，则该四棱锥外接球的表面积为（）10/56A．B．C．D．【答案】C【解析】由题意，四棱锥中，四边形是边长为2的正方形，且平面，可把四棱锥放置在如图所示的一个长方体内，其中长方体的长、宽、高分别为，则四棱锥的外接球和长方体的外接球表示同一个球，设四棱锥的外接球的半径为，可得，解得，所以该四棱锥外接球的表面积为.故选：C.【举一反三】1．（2020·广州市广外）各顶点都在一个球面上的正四棱柱（底面是正方形，侧棱垂直于底面）高为2，体积为8，则这个球的表面积是（）A．B．C．D．11/56【答案】B【解析】因为正四棱柱高为2，体积为8，所以它的底面边长是2，所以它的体对角线的长是，因此它的外接球的直径是，所以这个球的表面积是：.故选：B．2．（2020·辽宁省高三）如图，在三棱锥A﹣BCD中，BD⊥平面ADC，BD＝1，AB＝2，BC＝3，AC＝，则三棱锥A﹣BCD外接球的体积为（）A．4πB．3πC．2πD．4π【答案】D【解析】因为BD⊥平面ADC，所以，，所以，，所...