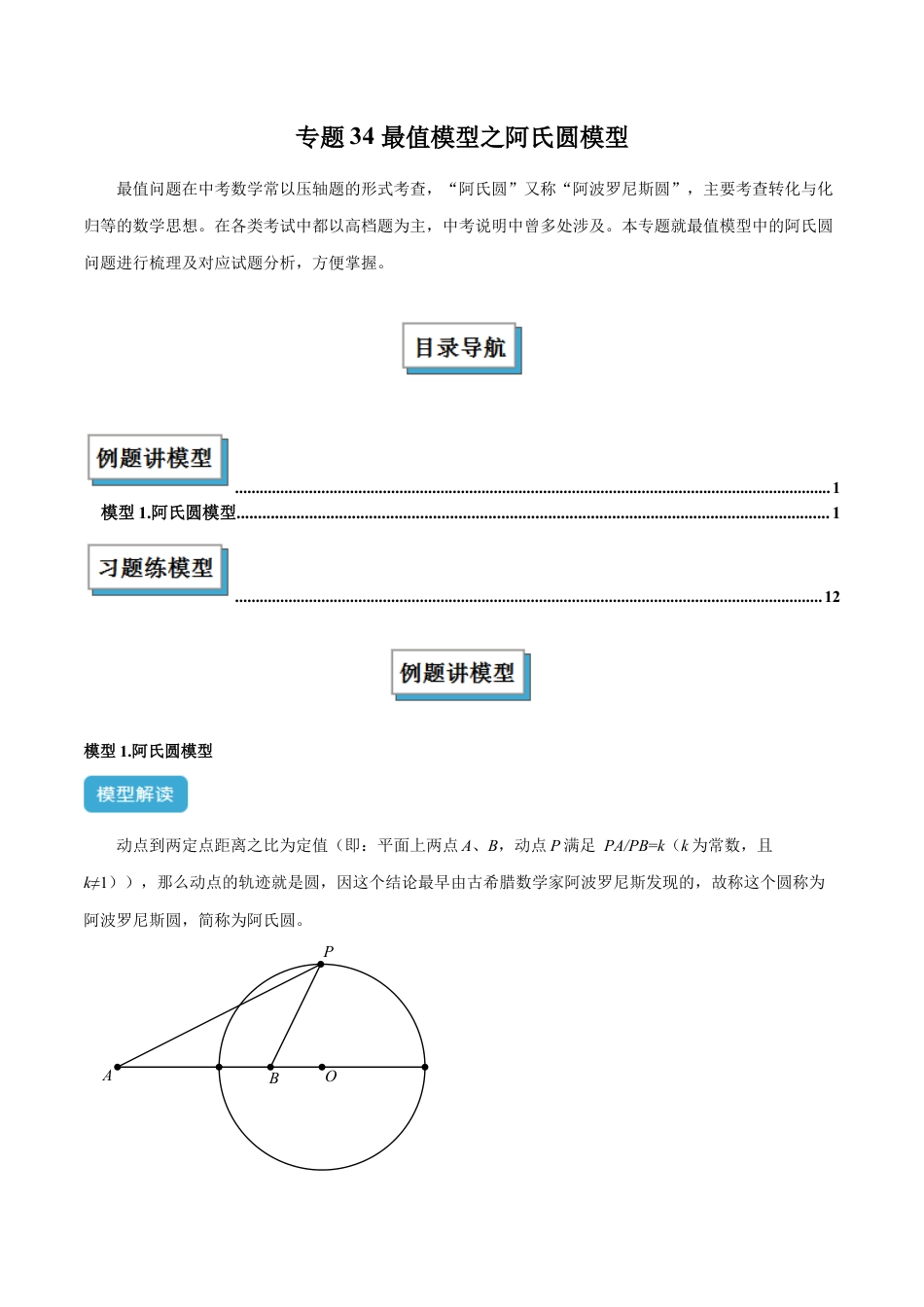
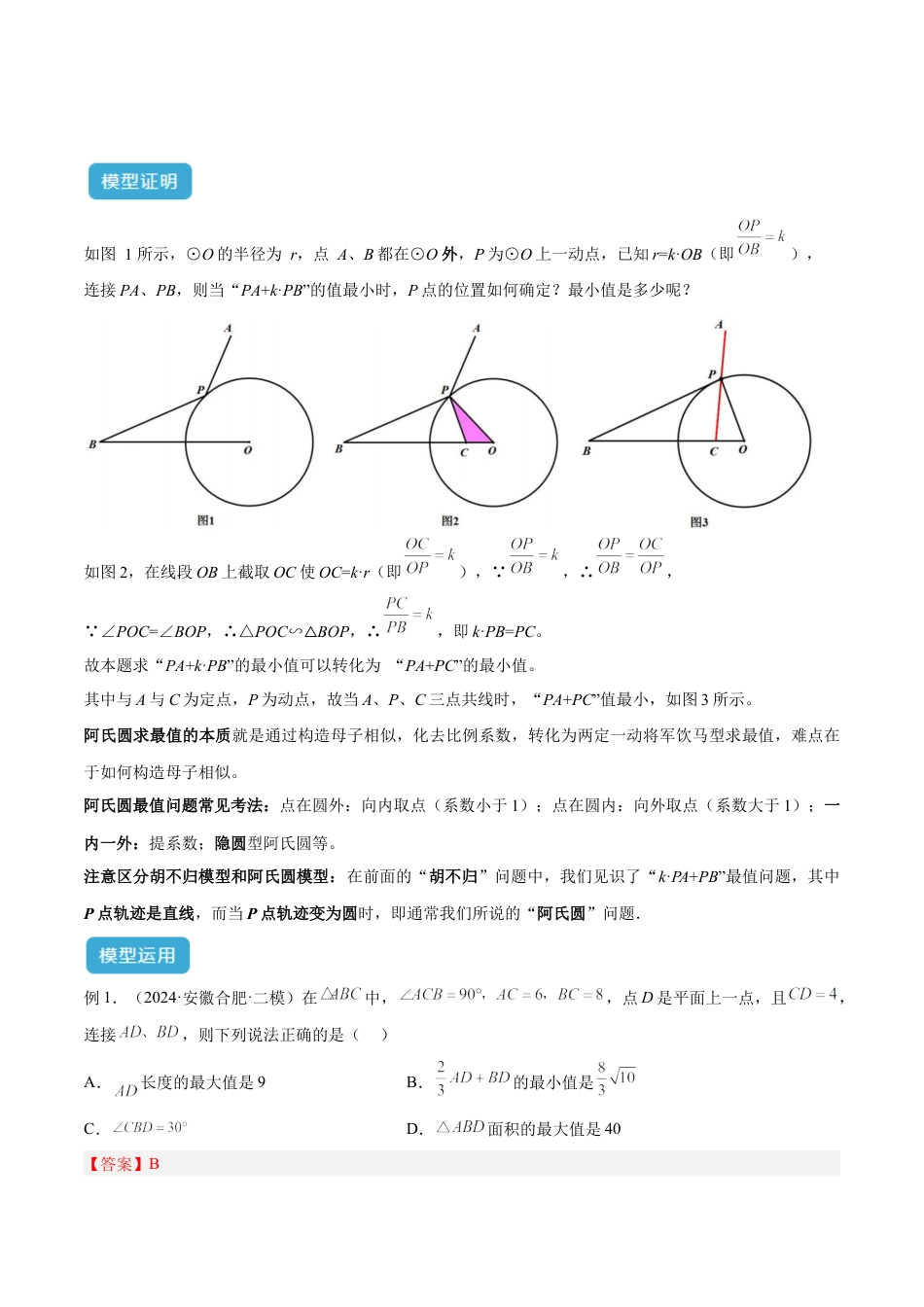
专题34最值模型之阿氏圆模型最值问题在中考数学常以压轴题的形式考查，“阿氏圆”又称“阿波罗尼斯圆”，主要考查转化与化归等的数学思想。在各类考试中都以高档题为主，中考说明中曾多处涉及。本专题就最值模型中的阿氏圆问题进行梳理及对应试题分析，方便掌握。.................................................................................................................................................1模型1.阿氏圆模型...........................................................................................................................................1...............................................................................................................................................12模型1.阿氏圆模型动点到两定点距离之比为定值（即：平面上两点A、B，动点P满足PA/PB=k（k为常数，且k≠1）），那么动点的轨迹就是圆，因这个结论最早由古希腊数学家阿波罗尼斯发现的，故称这个圆称为阿波罗尼斯圆，简称为阿氏圆。ABPO如图1所示，⊙O的半径为r，点A、B都在⊙O外，P为⊙O上一动点，已知r=k·OB（即），连接PA、PB，则当“PA+k·PB”的值最小时，P点的位置如何确定？最小值是多少呢？如图2，在线段OB上截取OC使OC=k·r（即）， ，∴， ∠POC=∠BOP，∴△POC∽△BOP，∴，即k·PB=PC。故本题求“PA+k·PB”的最小值可以转化为“PA+PC”的最小值。其中与A与C为定点，P为动点，故当A、P、C三点共线时，“PA+PC”值最小，如图3所示。阿氏圆求最值的本质就是通过构造母子相似，化去比例系数，转化为两定一动将军饮马型求最值，难点在于如何构造母子相似。阿氏圆最值问题常见考法：点在圆外：向内取点（系数小于1）；点在圆内：向外取点（系数大于1）；一内一外：提系数；隐圆型阿氏圆等。注意区分胡不归模型和阿氏圆模型：在前面的“胡不归”问题中，我们见识了“k·PA+PB”最值问题，其中P点轨迹是直线，而当P点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．例1．（2024·安徽合肥·二模）在中，，点D是平面上一点，且，连接，则下列说法正确的是（）A．长度的最大值是9B．的最小值是C．D．面积的最大值是40【答案】B【分析】本题考查了相似三角形判定与性质、勾股定理、点和圆的位置关系等知识，牢记相关性质是解题关键，根据点和圆的位置关系直接判断A、C、D，根据相似三角形判定与性质及勾股定理、两点之间线段最短判断B即可．【详解】解：A、，点D是平面上一点，且，点A、C、D在同一直线上且D在延长线上时，长度的最大值是，故本选项不符合题意；B、在上取点E，使，连接，当B、D、E共线时最小，此时，，故本选项符合题意；C、点D是平面上一点，且，点在以点C为圆心，4为半径的圆上，随着点D的变化而变化，故本选项不符合题意；D、点在以点C为圆心，4为半径的圆上，如下图，当所在直线垂直于时，面积的最大，在中，，，，，，，面积的最大值是44，故本选项不符合题意；故选：B．例2．（2024·广东·模拟预测）如图，已知正方ABCD的边长为6，圆B的半径为3，点P是圆B上的一个动点，则的最大值为_______．ABCDP【答案】【解析】当P点运动到BC边上时，此时PC=3，根据题意要求构造，在BC上取M使得此时PM=，则在点P运动的任意时刻，均有PM=，从而将问题转化为求PD-PM的最大值．连接PD，对于△PDM，PD-PM＜DM，故当D、M、P共线时，PD-PM=DM为最大值．ABCDPMMPDCBAABCDPMMPDCBA例3.（2023·北京·九年级专题练习）如图，边长为4的正方形，内切圆记为⊙O，P是⊙O上一动点，则PA＋PB的最小值为________．【答案】【分析】PA＋PB＝（PA＋PB），利用相似三角形构造PB即可解答．【详解】解：设⊙O半径为r，OP＝r＝BC＝2，OB＝r＝2，取OB的中点I，连接PI，∴OI＝IB＝， ，，∴，∠O是公共角，∴△BOP∽△POI，∴，∴PI＝PB，∴AP＋PB＝AP＋PI，∴当A、P、I在一条直线上时，AP＋PB最小，作IE⊥AB于E， ∠ABO＝45°，∴IE＝BE＝BI＝1，∴AE＝AB−BE＝3，∴AI＝，∴AP＋PB最小值＝AI＝， PA＋PB＝（PA＋PB），∴PA＋PB的最小值是AI＝．...