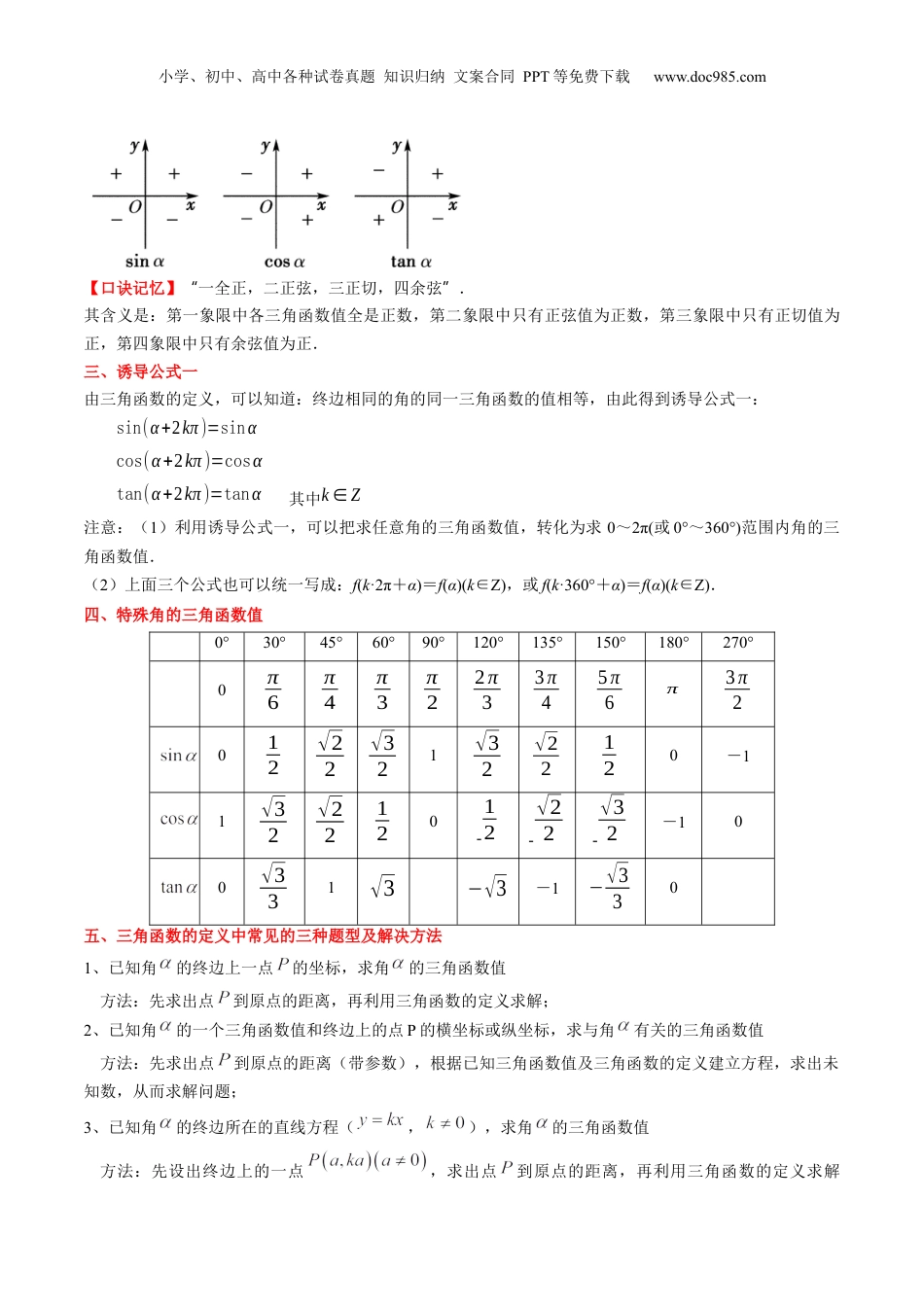
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第22讲三角函数的概念1．借助单位圆理解任意角的三角函数（正弦、余弦、正切）的含义；2．掌握任意角的三角函数值在各象限的符号；3．会利用角的终边上的点的坐标求角的正弦、余弦和正切；4．掌握公式一并会应用一、三角函数的定义1、定义：设α是一个任意角，它的终边与单位圆交于点P(x,y)，则：叫做的正弦函数，记作.即；叫做的余弦函数，记作.即；叫做的正切函数，记作.即。2、三角函数定义域正弦函数、余弦函数、和正切函数统称为三角函数，通常记为：正弦函数：余弦函数：正切函数：3、三角函数另一种情况若已知角α终边上一点（不与原点重合）不是以坐标原点为圆心的单位圆上的点，先求，则，，.三角函数值只与角的大小有关，而与终边上点P的位置无关。二、三角函数的符号小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【口诀记忆】一全正，二正弦，三正切，四余弦．“”其含义是：第一象限中各三角函数值全是正数，第二象限中只有正弦值为正数，第三象限中只有正切值为正，第四象限中只有余弦值为正．三、诱导公式一由三角函数的定义，可以知道：终边相同的角的同一三角函数的值相等，由此得到诱导公式一：sin(α+2kπ)=sinαcos(α+2kπ)=cosαtan(α+2kπ)=tanα其中k∈Z注意：（1）利用诱导公式一，可以把求任意角的三角函数值，转化为求0～2π(或0°～360°)范围内角的三角函数值．（2）上面三个公式也可以统一写成：f(k·2π＋α)＝f(α)(k∈Z)，或f(k·360°＋α)＝f(α)(k∈Z)．四、特殊角的三角函数值0°30°45°60°90°120°135°150°180°270°0π6π4π3π22π33π45π6π3π2012√22√321√32√22120－11√32√22120-12-√22-√32－100√331√3−√3－1−√330五、三角函数的定义中常见的三种题型及解决方法1、已知角的终边上一点的坐标，求角的三角函数值方法：先求出点到原点的距离，再利用三角函数的定义求解；2、已知角的一个三角函数值和终边上的点P的横坐标或纵坐标，求与角有关的三角函数值方法：先求出点到原点的距离（带参数），根据已知三角函数值及三角函数的定义建立方程，求出未知数，从而求解问题；3、已知角的终边所在的直线方程（，），求角的三角函数值方法：先设出终边上的一点，求出点到原点的距离，再利用三角函数的定义求解小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（注意的符号，对分类讨论）考点一：由终边或终边上的点求三角函数例1．若角的终边经过点，则的值为（）A．B．C．D．【答案】A【解析】因为角的终边上有一点，所以，故选：A【变式训练】已知角以坐标系中为始边，终边与单位圆交于点，则下列各式正确的有（）A．B．C．D．【答案】C【解析】因为角以坐标系中为始边，终边与单位圆交于点，所以，所以，故A错误；，故B错误；，故C正确；，故D错误.故选：C.考点二：由三角函数值求终边上点的参数例2．角的终边经过点且，则b的值为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．3B．C．D．5【答案】B【解析】根据三角函数定义可得，且，即，解得．故选：B．【变式训练】若是第二象限角，为其终边上一点，，则值为（）A．B．C．D．【答案】C【解析】由三角函数的定义，可得，解得，即，则，所以.故选：C.考点三：三角函数的符号判断例3．已知且，则的终边在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】A【解析】 已知，∴的终边在第一或第三象限．若的终边在第一象限，则，故，满足题意，若的终边在第三象限，则，故，不满足题意，∴的终边在第一象限.故选：A．【变式训练】确定下列各式的符号（1）)；（2）.【答案】（1）负号；（2）负号【解析】（1）因为是第二象限角，所以，因为是第三象限角，所以，所以，即的符号为负号.（2）因为，所以5是第四象限角，所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com又因为，所以，所以，所以的符号为负号.考点四：圆上的动点与旋转点例4．点在圆上沿逆时针方向...