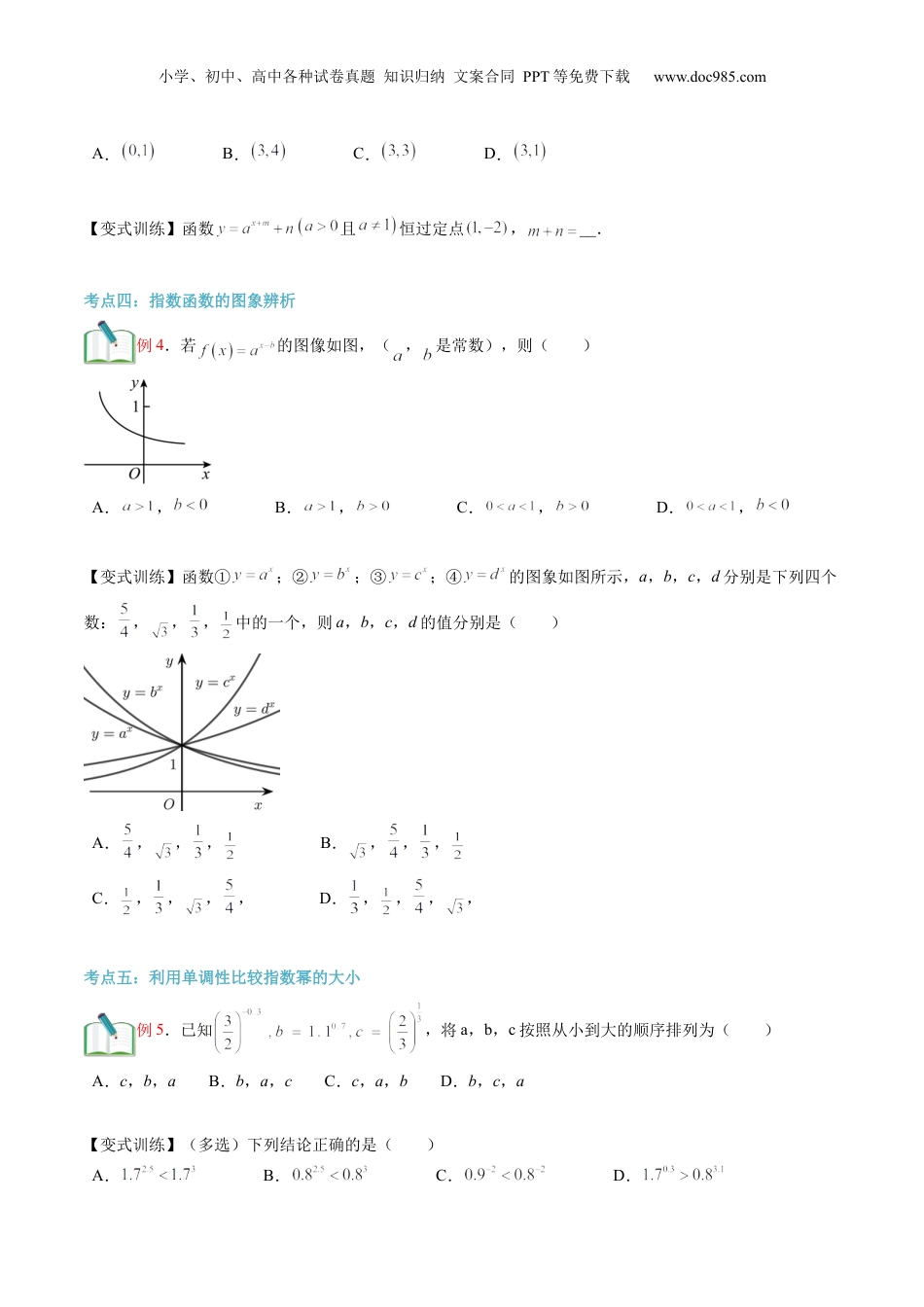
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第14讲指数函数及其性质1．理解指数函数的概念，掌握指数函数的定义域、值域的求法；2．理解指数函数的单调性，能利用指数函数的单调性比较幂的大小；3．掌握指数函数图象通过的特殊的点，会作指数函数的图象，掌握指数函数的性质。一、指数函数的概念1、定义：一般地，函数（且）叫做指数函数，其中指数x是自变量，定义域是R，a是指数函数的底数．2、注意事项：指数函数的底数规定大于0且不等于1的理由：（1）如果，当（2）如果，如，当时，在实数范围内函数值不存在．（3）如果，是一个常量，对它就没有研究的必要．为了避免上述各种情况，所以规定且．二、指数函数的图象与性质a>10<a<1图象性质定义域R值域(0,+∞)过定点(0,1)单调性在上是增函数在上是减函数奇偶性非奇非偶函数三、比较指数幂的大小小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com比较幂的大小的常用方法：（1）对于底数相同，指数不同的两个幂的大小比较，可以利用指数函数的单调性来判断；（2）对于底数不同，指数相同的两个幂的大小比较，可以利用指数函数图象的变化规律来判断；（3）对于底数不同，且指数也不同的幂的大小比较，可先化为同底的两个幂，或者通过中间值来比较．四、简单指数不等式的解法1、形如的不等式，可借助的单调性求解；2、形如的不等式，可将化为为底数的指数幂的形式，再借助的单调性求解；3、形如的不等式，可借助两函数，的图象求解。考点一：指数函数的概念辨析例1．（多选）下列函数中，是指数函数的是（）A．B．C．D．【变式训练】（多选）下列函数是指数函数的是（）A．B．C．D．且考点二：利用指数函数的概念求参例2．若函数为指数函数，则a的取值范围是________【变式训练】若函数为指数函数，则（）A．或B．且C．D．考点三：指数函数过定点问题例3．函数恒过定点（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【变式训练】函数且恒过定点，__．考点四：指数函数的图象辨析例4．若的图像如图，（，是常数），则（）A．，B．，C．，D．，【变式训练】函数①；②；③；④的图象如图所示，a，b，c，d分别是下列四个数：，，，中的一个，则a，b，c，d的值分别是（）A．，，，B．，，，C．，，，，D．，，，，考点五：利用单调性比较指数幂的大小例5．已知，将a，b，c按照从小到大的顺序排列为（）A．c，b，aB．b，a，cC．c，a，bD．b，c，a【变式训练】（多选）下列结论正确的是（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点六：解指数型不等式例6．不等式的解集是（）A．B．C．D．【变式训练】解关于的不等式．考点七：指数型函数的单调性例7．函数的单调递增区间是（）A．B．[2，＋）∞C．D．【变式训练】函数的单调递增区间为______.考点八：指数型函数的奇偶性例8．函数的奇偶性是（）A．是奇函数，不是偶函数B．是偶函数，不是奇函数C．既是奇函数，也是偶函数D．非奇非偶函数【变式训练】已知为偶函数，则实数（）A．1B．-1C．0D．考点九：指数型函数的值域例9．函数的值域为______.【变式训练】函数在区间［-1，1］上的最大值为___________.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．如果函数和都是指数函数，则（）A．B．1C．9D．82．函数的图像不经过（）A．第一象限B．第二象限C．第三象限D．第四象限3．函数（其中，，、为常数）的图像恒过定点，则（）A．3B．4C．5D．64．函数的单调递增区间是（）A．B．C．D．5．如图所示：曲线，，和分别是指数函数，,和的图象,则a，b，c，d与1的大小关系是（）A．B．C．D．6．已知有三个数，，，则它们的大小关系是（）A．B．C．D．7．不等式的解集为（）A．B．C．D．8．（多选）已知函数，则（）A．的值域为B．是上的增函数C．是上的奇函数D．有最大值小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com9．（多选）函数其中且，则下列结论正确的是（）A．函数是奇函...