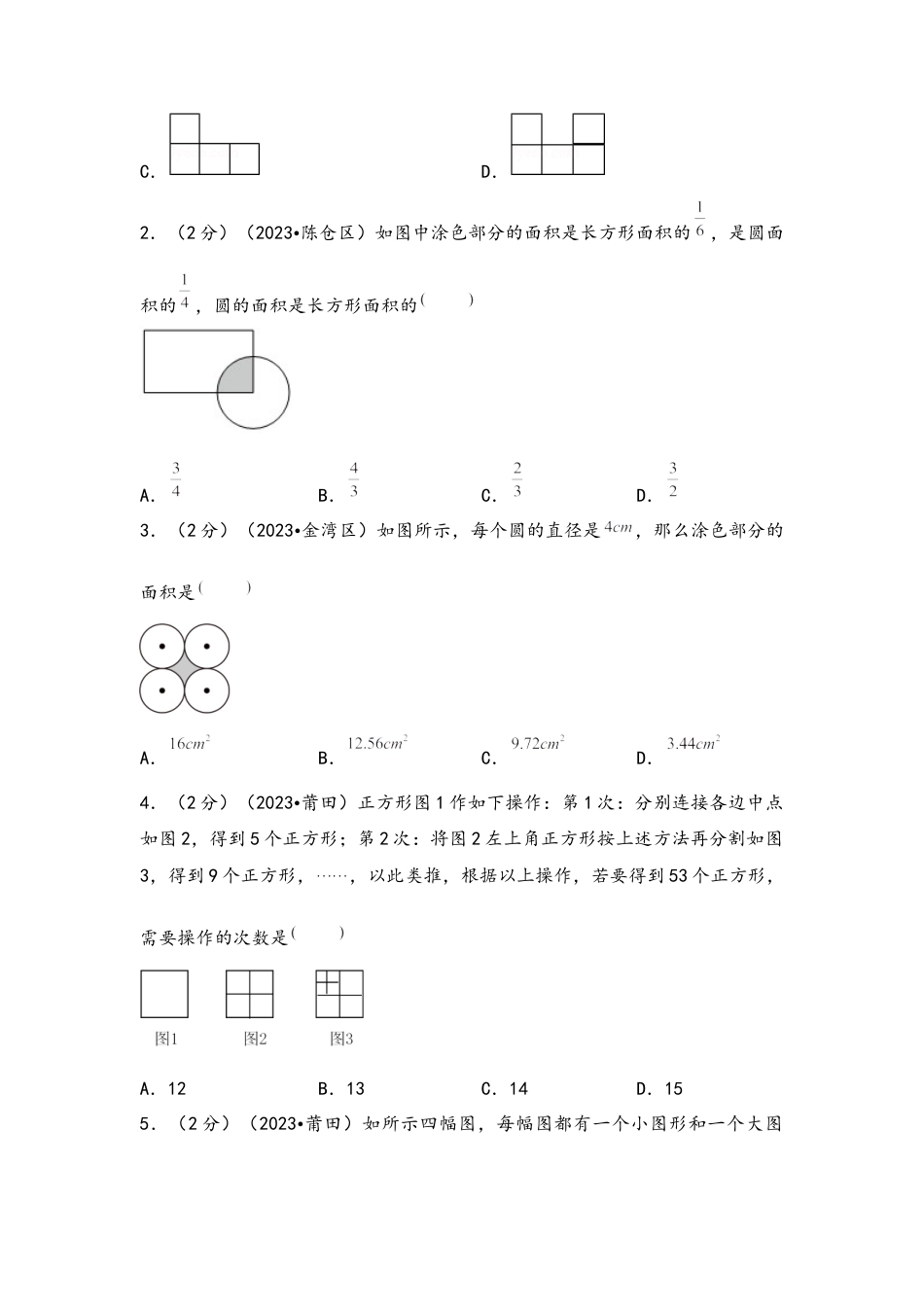
专题60组合图形（考点聚焦+重点速记+真题专练）一、平面图形的切拼。1.图形的剪拼，即把一个几何图形剪成几块形状相同的图形，或是把一个几何图形剪开后拼成另一种满足某种条件的图形。完成这样的图形剪拼，需要考虑图形剪开各部分的形状、大小以及它们之间的位置关系。2.在拼图形的过程中，要从图形的性质入手，观察它的对称点，对称轴，从这些性质出发解决问题。二、图形的拼组。1．平面镶嵌的概念：用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地拼接在一起，这就是平面镶嵌．2．规律：用相同的正多边形镶嵌：只用一种多边形时，可以进行镶嵌的是三角形、四边形或正六边形．用不同的正多边形镶嵌：（1）用正三角形和正六边形能够进行平面镶嵌；（2）用正十二边形、正六边形，正方形能够进行平面镶嵌．三、简单的立方体切拼问题。1．拼起来，表面积减小，因为面的数目减少．2．剪切会增加表面积，因为面的数目增加．3．两种方式的体积都没有发生变化．四、图形的密铺。用形状、大小完全相同的几种或几十种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的密铺，又称做平面图形的镶嵌．①正多边形密铺：正六边形可以密铺，因为它的每个内角都是120°度，在每个拼接点处恰好能容纳3个内角；正五边形不可以密铺，因为它的每个内角都是108度，而360°不是108的整数倍，在每个拼接点处的内角不能保证没空隙或重叠现象；除正三角形、正四边形和正六边形外，其它正多边形都不可以密铺平面．②不可单独密铺的图形：a、所有任意三角形与任意四边形都可以密铺．b、正三角形、正四边形、正六边形可以单独用于平移密铺．c、三对对应边平行的六边形可以单独密铺．一．选择题（共8小题，满分16分，每小题2分）1．（2分）（2021•阜宁县）下图是由5个相同的正方体木块搭成的几何体，从上面看到的图形是A．B．C．D．2．（2分）（2023•陈仓区）如图中涂色部分的面积是长方形面积的，是圆面积的，圆的面积是长方形面积的A．B．C．D．3．（2分）（2023•金湾区）如图所示，每个圆的直径是，那么涂色部分的面积是A．B．C．D．4．（2分）（2023•莆田）正方形图1作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形，，以此类推，根据以上操作，若要得到53个正方形，需要操作的次数是A．12B．13C．14D．155．（2分）（2023•莆田）如所示四幅图，每幅图都有一个小图形和一个大图形。下面描述不正确的是A．每幅图中，大图形都是由小图形累加得到。B．每幅图中，小图形都可以用来测量大图形。C．大图形里包含几个小图形，测量的结果就是几。D．每幅图中，大图形都是由9个小图形组成。6．（2分）（2023•龙港市）如图，至少添上个小正方体，就能拼成一个大正方体。A．11B．16C．25D．277．（2分）（2023•永嘉县）文文家的客厅长3.6米，宽3.3米。要给这间客厅铺地砖，下面哪一种地砖可以不用切割，正好密铺？A．B．C．D．8．（2分）（2023•齐河县）下面图，和正好拼成一个棱长为2的大正方体。（每个小正方体的棱长为A．B．C．D．二．填空题（共8小题，满分16分，每小题2分）9．（2分）（2023•东阿县）如图所示，把一个高为10厘米的圆柱切成若干等份，拼成一个近似的长方体．如果这个长方体的底面积是50平方厘米，那么圆柱体积是立方厘米．10．（2分）（2023•福清市）如图，两个同心圆中间有一个正方形，正方形的面积是10平方厘米，外圆的面积是平方厘米，外圆的面积与内圆的面积比是11．（2分）（2023•漳州）一张长方形纸长、宽，用它剪半径的圆，最多可以剪个。12．（2分）（2021•兴义市）数学课上小兰要在一张正方形纸片上剪一个面积是的圆形，她至少要准备一张面积的正方形纸片。13．（2分）（2021•瑞金市）用圆规画周长为的圆，圆规两脚间的距离应该是，若在一块长、宽的卡纸上，最多可剪个这样的圆片。14．（2分）（2023•海城市）如图所示，如果圆的直径是6厘米，那么正方形的面积是平方厘米．15．（2分）（2023•南平）如图，用“十字形”分割正方形，分割...