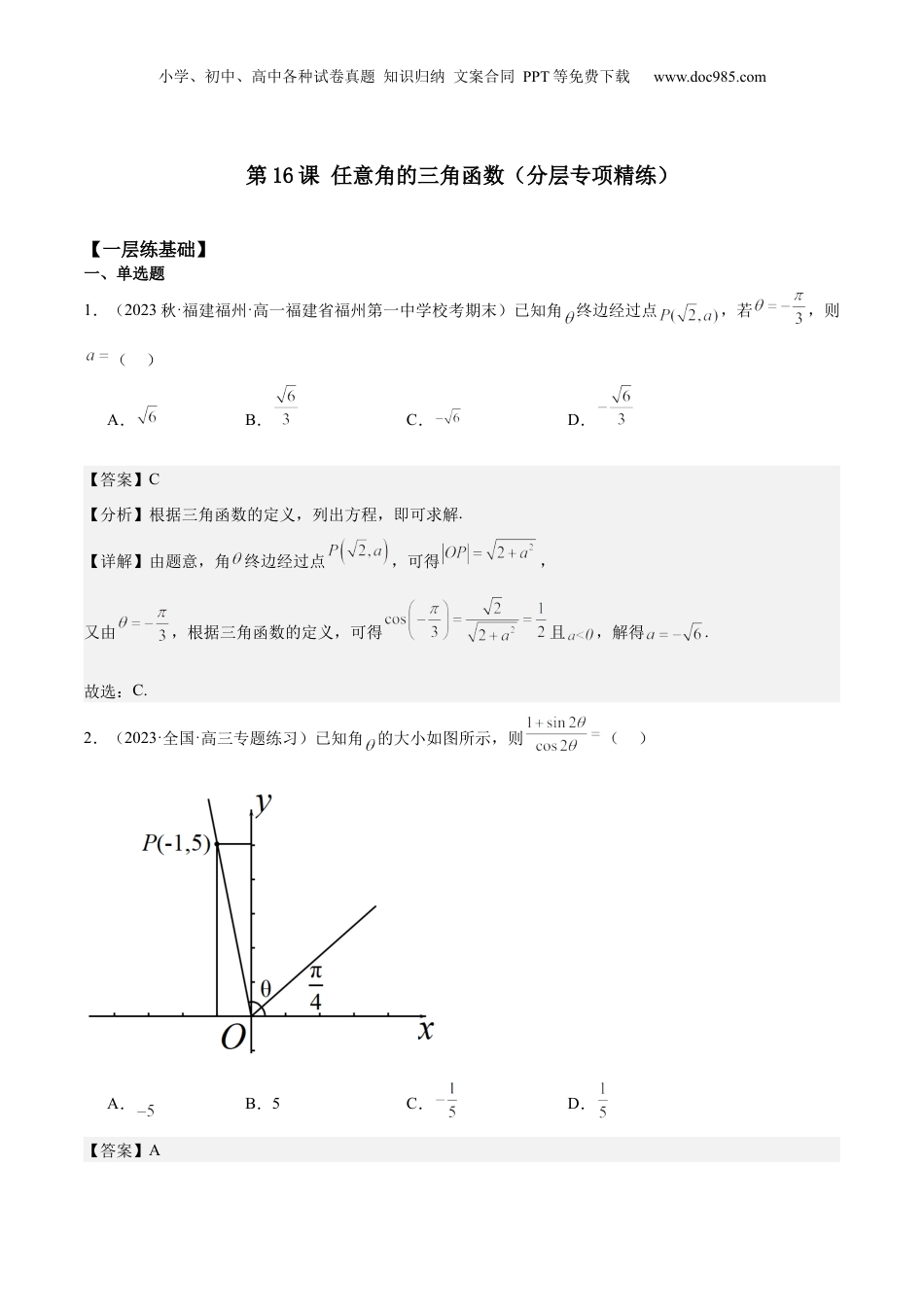
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第16课任意角的三角函数（分层专项精练）【一层练基础】一、单选题1．（2023秋·福建福州·高一福建省福州第一中学校考期末）已知角终边经过点，若，则（）A．B．C．D．【答案】C【分析】根据三角函数的定义，列出方程，即可求解.【详解】由题意，角终边经过点，可得，又由，根据三角函数的定义，可得且，解得.故选：C.2．（2023·全国·高三专题练习）已知角的大小如图所示，则（）A．B．5C．D．【答案】A小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】由图中的信息可知，化简即可.【详解】由图可知，，；故选：A.3．（2023春·北京·高一校考期中）如图，角以为始边，它的终边与单位圆相交于点，且点的横坐标为，则的值为（）A．B．C．D．【答案】B【分析】由题意利用任意角的三角函数的定义，求得的值．【详解】角以为始边，它的终边与单位圆相交于点，且点的横坐标为，所以则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com；故选：B．【点睛】本题主要考查任意角的三角函数的定义，属于基础题．4．（2023春·江苏宿迁·高一校考阶段练习）已知锐角的终边上一点的坐标为，则＝（）A．40°B．45°C．50°D．55°【答案】C【分析】利用二倍角公式化简，即可得到，根据三角函数的定义及的范围判断即可；【详解】解：因为锐角的终边上一点的坐标为，且，，从而有点的坐标为，所以．故选：C．二、多选题5．（2022·高一课时练习）已知平面向量，，，则下列说法正确的是（）A．若，则或B．的充要条件是C．若，则D．若，则【答案】AB【分析】利用平面向量垂直的坐标表示可判断A选项；利用平面向量共线的坐标表示可判断B选项；利用小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com平面向量数量积的坐标运算可判断C选项；利用平面向量的模长公式可判断D选项.【详解】对于A，若，则，解得，因为，所以或，故A正确；对于B，若，则，解得或（舍去），因为，所以，即，当时，，，，则，即，故B正确；对于C，若，则，解得，因为，所以，故C错误；对于D，若，则，整理得，解得或，因为，所以或或，故D错误.故选：AB.6．（2023秋·高一课时练习）在平面直角坐标系中，角顶点在原点，以正半轴为始边，终边经过点，则下列各式的值恒大于0的是（）A．B．C．D．【答案】AB【分析】根据角终边经过点，结合三角函数的定义可以判断角的正弦、余弦、正切的正负性，对四个选项逐一判断即可选出正确答案.【详解】由题意知角在第四象限，所以，，.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com选项A，；选项B，；选项C，；选项D，符号不确定.故选：AB.7．（2023·全国·高三专题练习）已知角的终边与单位圆交于点，则（）A．B．C．D．【答案】AC【分析】点代入单位圆的方程求出点可得，再由弦化切可得答案.【详解】角的终边与单位圆交于点，，，，当时，；当时，．故选：AC.三、填空题8．（2023春·四川泸州·高一四川省泸县第四中学校考阶段练习）在平面直角坐标系中，点绕着原点顺时针旋转得到点，点的横坐标为.【答案】【分析】根据三角函数定义求得，确定与x轴正半轴的夹角为,结合三角函数定义以及两角差的余弦公式即可求得答案.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】由题意得,设与x轴正半轴的夹角为，则，则与x轴正半轴的夹角为，故点的横坐标为，故答案为：9．（2020秋·江苏泰州·高三江苏省姜堰第二中学校考阶段练习）欧拉公式（为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它不仅出现在数学分析里，而且在复变函数论里也占有非常重要的地位，被誉为“数学中的天桥”.根据欧拉公式可知，表示的复数在复平面中位于第象限.【答案】三【分析】由欧拉公式可得，则表示的复数在复平面中对应的点为.判断点所在的象限，即得答案.【详解】由欧拉公式可得，则表示的复数在复平面中对应的点为....