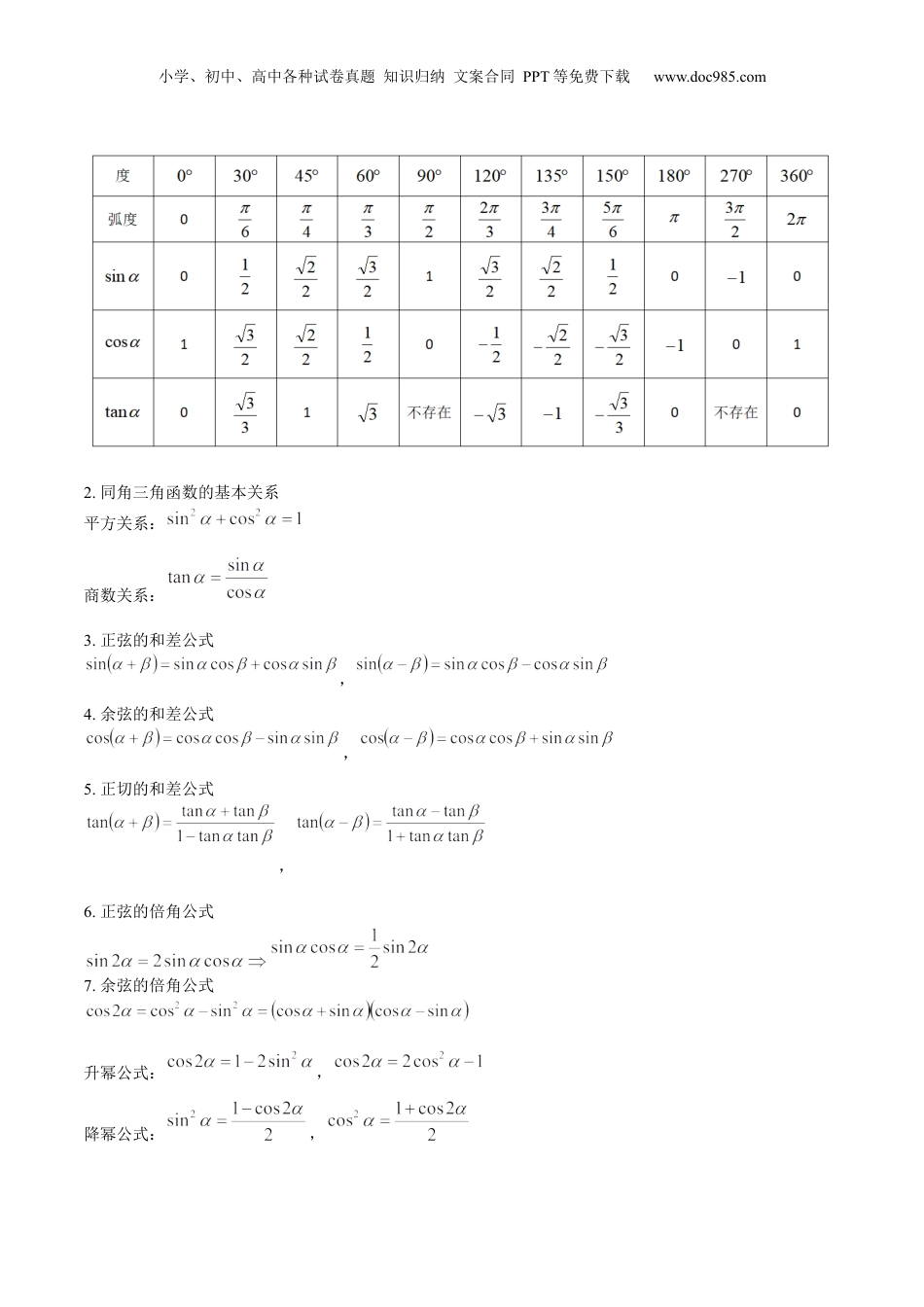
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com押新高考5题三角函数与解三角形考点4年考题考情分析三角函数与解三角形2023年新高考Ⅰ卷第8、15题2023年新高考Ⅱ卷第7、16题2022年新高考Ⅰ卷第6题2022年新高考Ⅱ卷第6题2021年新高考Ⅰ卷第6题2020年新高考Ⅰ卷第10、15题2020年新高考Ⅱ卷第11、16题三角函数与解三角形会以单选题、多选题、填空题、解答题4类题型进行考查，单选题难度较易或一般，纵观近几年的新高考试题，分别考查三角函数的图象与性质，三角恒等变换，本内容是新高考冲刺的重点复习内容。可以预测2024年新高考命题方向将继续以三角函数的图象与性质、值域及参数范围、三角恒等变换、解三角形及其实际应用等问题展开命题．1．（2023·新高考Ⅰ卷高考真题第8题）已知，则（）．A．B．C．D．2．（2023·新高考Ⅰ卷高考真题第15题）已知函数在区间有且仅有3个零点，则的取值范围是．3．（2023·新高考Ⅱ卷高考真题第7题）已知为锐角，，则（）．A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4．（2023·新高考Ⅱ卷高考真题第16题）已知函数，如图A，B是直线与曲线的两个交点，若，则．5．（2022·新高考Ⅰ卷高考真题第6题）记函数的最小正周期为T．若，且的图象关于点中心对称，则（）A．1B．C．D．36．（2022·新高考Ⅱ卷高考真题第6题）若，则（）A．B．C．D．7．（2021·新高考Ⅰ卷高考真题第6题）若，则（）A．B．C．D．1.特殊角的三角函数值小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2.同角三角函数的基本关系平方关系：商数关系：3.正弦的和差公式，4.余弦的和差公式，5.正切的和差公式，6.正弦的倍角公式7.余弦的倍角公式升幂公式：，降幂公式：，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8.正切的倍角公式9.推导公式10.辅助角公式，，其中，11.正弦定理（1）基本公式：（其中为外接圆的半径）（2）变形12.三角形中三个内角的关系，，13.余弦定理（1）边的余弦定理，，（2）角的余弦定理，，14.三角形的面积公式小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．（2024·广东湛江·二模）函数在上的值域为（）A．B．C．D．2．（2024·全国·二模）若函数的图象关于轴对称，则（）A．B．C．D．3．（2024·山东济南·一模）已知a，b，c分别为三个内角A，B，C的对边，且，则（）A．B．C．D．4．（2024·黑龙江齐齐哈尔·二模）在中，，，则（）A．B．C．D．5．（2024·辽宁大连·一模）若，且，则（）A．B．C．D．16．（2024·贵州·模拟预测）如图，甲秀楼位于贵州省贵阳市南明区甲秀路，是该市的标志性建筑之一.甲秀楼始建于明朝，后楼毁重建，改名“凤来阁”，清代甲秀楼多次重修，并恢复原名、现存建筑是宣统元年（1909年）重建.甲秀楼上下三层，白石为栏，层层收进.某研究小组将测量甲秀楼最高点离地面的高度，选取了与该楼底在同一水平面内的两个测量基点与，现测得，，，在点测得甲秀楼顶端的仰角为，则甲秀楼的高度约为（参考数据：，）（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．7．（2024·湖南·模拟预测）湖南省衡阳市的来雁塔，始建于明万历十九年（1591年），因鸿雁南北迁徙时常在境内停留而得名.1983年被湖南省人民政府公布为重点文物保护单位.为测量来雁塔的高度，因地理条件的限制，分别选择C点和一建筑物DE的楼顶E为测量观测点，已知点A为塔底，在水平地面上，来雁塔AB和建筑物DE均垂直于地面（如图所示）.测得，在C点处测得E点的仰角为30°，在E点处测得B点的仰角为60°，则来雁塔AB的高度约为（）（，精确到）A．B．C．D．8．（2024·云南·一模）已知，则（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com9．（2024·全国·模拟预测）已知，则（）A．B．C．D．10．（2024·重庆·模拟预测）已知角θ满足，则（）A．B．C．D．11．（2024·全国·模拟预测）已知为锐角，，则（）A．B...