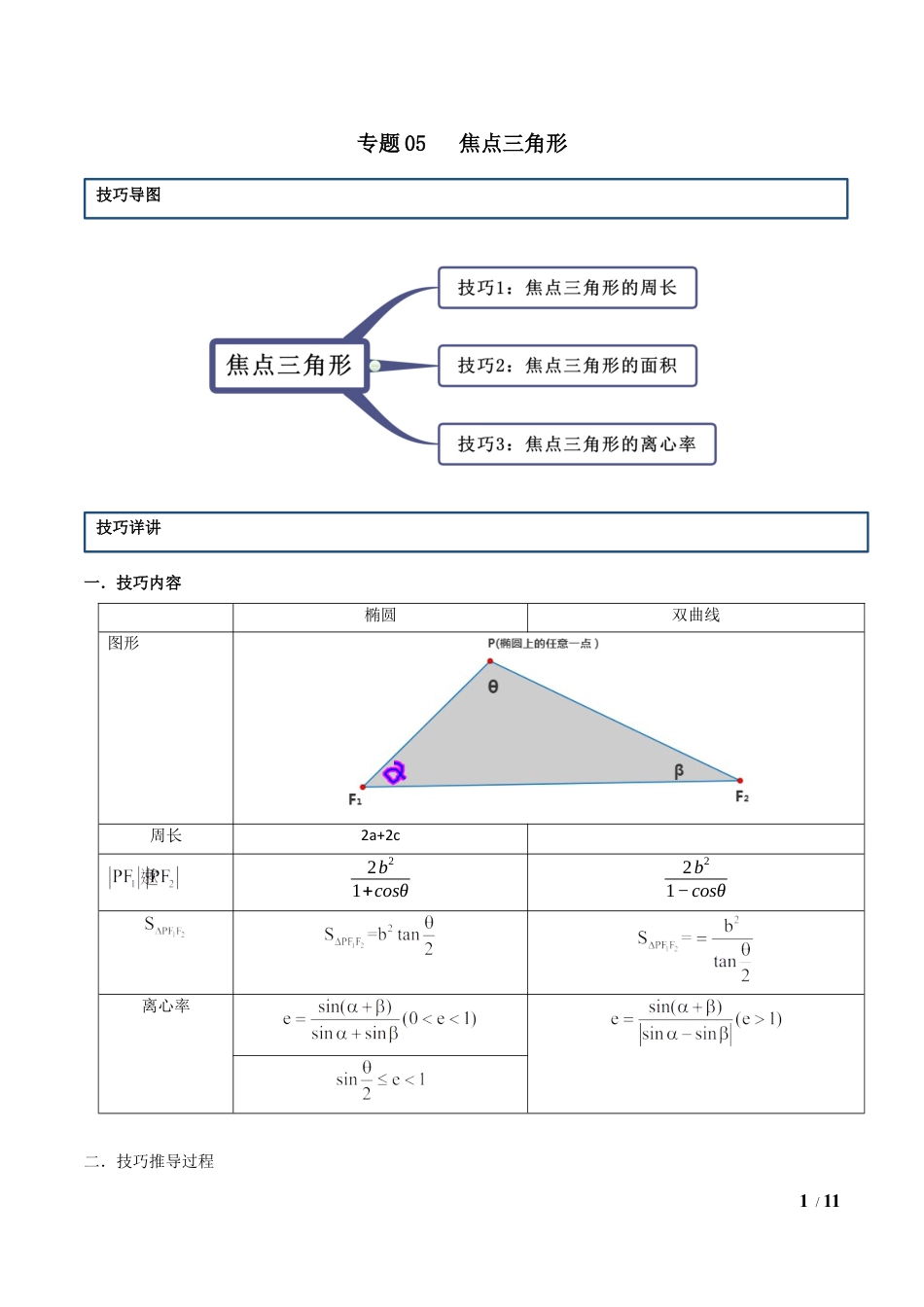
1/11专题05焦点三角形一．技巧内容二．技巧推导过程技巧导图技巧详讲椭圆双曲线图形周长2a+2c2b21+cosθ2b21−cosθ离心率2/111.2.椭圆中焦点三角形的面积公式3.椭圆中的离心率4.3/115.双曲线中焦点三角形的面积公式6.双曲线中的离心率技巧1焦点三角形的周长【例1】（2020·黑龙江）已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于（）A．20B．16C．18D．14【举一反三】1．（2020·西藏南木林县第一中学高三月考）若椭圆（其中a＞b＞0）的离心率为，两焦点分别为F1，F2，M为椭圆上一点，且△F1F2M的周长为16，则椭圆C的方程为（）A．B．C．D．例题举证4/112．（2019·广西南宁）定义：椭圆上一点与两焦点构成的三角形为椭圆的焦点三角形，已知椭圆的焦距为，焦点三角形的周长为，则椭圆的方程是__________．技巧2焦点三角形的面积【例2-1】（2020·安徽省定远中学）已知椭圆的左、右焦点分别为、，为椭圆上一点，且，若的面积为9，则__________．【例2-2】（2020·山西大同）已知、为双曲线的左、右焦点，点P在C上，，则的面积为【举一反三】1．（2020·云南陆良）已知、为双曲线C：的左、右焦点，点P在C上，∠P=，则（）A．2B．4C．6D．82（2020·广东汕头）若椭圆上一点P与椭圆的两个焦点、的连线互相垂直，则的面积为()A．36B．16C．20D．245/113．（2020·上海普陀·高三三模）设为双曲线（）的上一点，，（为左、右焦点），则的面积等于（）A．B．C．D．技巧3焦点三角形的离心率【例3-1】设椭圆的左、右焦点分别为,是上的点,,,则的离心率为()A.B.C.D.【例3-2】（2020·河北衡水中学）已知分别是椭圆的左、右焦点，若椭圆上存在点，使，则椭圆的离心率的取值范围为（）A．B．C．D．【举一反三】1．（2020·沙坪坝·重庆一中高三月考（理））已知点P在以为左，右焦点的椭圆上，在中，若，，则（）6/11A．B．C．D．2．（2020·安徽合肥·高三二模（文））记，为椭圆的两个焦点，若上存在点满足，则实数取值范围是()A．B．C．D．1．（2020·全国高三单元测试）已知F1，F2是椭圆＋＝1的两焦点，过点F2的直线交椭圆于A，B两点．在△AF1B中，若有两边之和是10，则第三边的长度为()A．6B．5C．4D．32．（2020·广西钦州一中）设椭圆C：(a>0，b>0)的左右焦点分别为､，，离心率为.P是C上一点，且⊥.若的面积为4，则a=（）A．1B．2C．4D．83．（2020·河南高三其他（文））椭圆的左、右焦点分别为，，椭圆上的技巧强化7/11点满足：，且，则（）A．1B．C．D．2.4．（2020·黑龙江绥化·高三其他（理））已知对任意正实数m，n，p，q，有如下结论成立：若，则有成立，现已知椭圆上存在一点P，，为其焦点，在中，，，则椭圆的离心率为（）A．B．C．D．5．（2020·山西临汾）已知椭圆的左，右焦点分别为，若上的点到的距离为，则△的面积为（）A．B．C．D．8/116．（2020·陆川中学）已知，分别是椭圆的左、右焦点，若椭圆上存在点，使得，则该椭圆的离心率的取值范围是（）A．B．C．D．7．（2020·全国高三一模（文））设椭圆的两焦点为，，若椭圆上存在点，使，则椭圆的离心率的最小值为（）A．B．C．D．8．（2019·江西南昌十中））已知点F1，F2分别是椭圆C1和双曲线C2的公共焦点，e1，e2分别是C1和C2的离心率，点P为C1和C2的一个公共点，且，若，则e1的取值范围是（）A．B．C．D．9．（2020·伊美区第二中学）设是双曲线的两个焦点,是双曲线上的一点,且,则的面积等于（）9/11A．B．C．24D．4810．（2020·四川青羊·树德中学高二月考（文））设、分别为双曲线的左、右焦点，双曲线上存在一点使得，，则该双曲线的离心率为（）A．B．C．D．11．（2020·吉林松原·高三其他（文））已知点是双曲线上一点，，分别为双曲线的左右焦点，若､的外接圆半径为4，且为锐角，则（）A．15B．16C．18D．2012．（2020·陕西省丹凤中学高三一模（理））设，分别是双曲线的左右焦点.若点在双曲线上，且，则等于（）A．B．C．D．13．（2020·陕西高三其他（文））已知双曲线：（，）的左、右焦点分别为10/11，，点在双曲线的右支上，若，则的取值范围是（）A．B．C．D．14．（2020·河北张家口·...