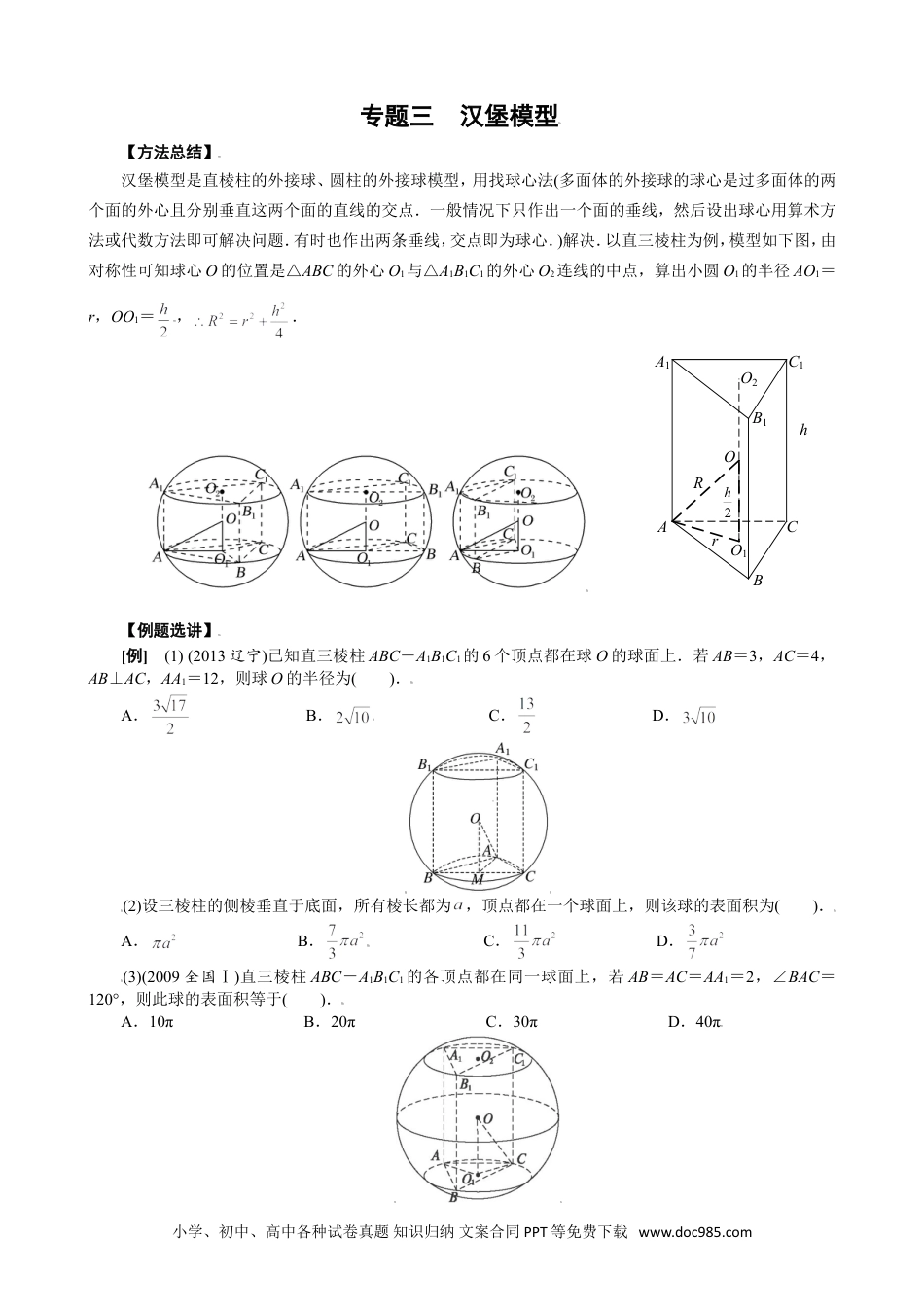
专题三汉堡模型【方法总结】汉堡模型是直棱柱的外接球、圆柱的外接球模型，用找球心法(多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点．一般情况下只作出一个面的垂线，然后设出球心用算术方法或代数方法即可解决问题．有时也作出两条垂线，交点即为球心．)解决．以直三棱柱为例，模型如下图，由对称性可知球心O的位置是△ABC的外心O1与△A1B1C1的外心O2连线的中点，算出小圆O1的半径AO1＝r，OO1＝，．O1C1AA1B1OBCRrh2hO2【例题选讲】[例](1)(2013辽宁)已知直三棱柱ABC－A1B1C1的6个顶点都在球O的球面上．若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为()．A．B．C．D．(2)设三棱柱的侧棱垂直于底面，所有棱长都为，顶点都在一个球面上，则该球的表面积为()．A．B．C．D．(3)(2009全国Ⅰ)直三棱柱ABC－A1B1C1的各顶点都在同一球面上，若AB＝AC＝AA1＝2，∠BAC＝120°，则此球的表面积等于()．A．10πB．20πC．30πD．40π小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(4)已知圆柱的高为2，底面半径为，若该圆柱的两个底面的圆周都在同一个球面上，则这个球的表面积等于()A．4πB．C．D．16π(5)若一个圆柱的表面积为，则该圆柱的外接球的表面积的最小值为A．B．C．D．【对点训练】1．一直三棱柱的每条棱长都是2，且每个顶点都在球O的表面上，则球O的表面积为()A．B．C．D．π2．一个正六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为，底面周长为3，则这个球的体积为________.3．已知正三棱柱ABC－A1B1C1中，底面积为，一个侧面的周长为6，则正三棱柱ABC－A1B1C1外接球的表面积为()A．4πB．8πC．16πD．32π4．已知直三棱柱ABC－A1B1C1的6个顶点都在球O的球面上，若AB＝3，AC＝1，∠BAC＝60°，AA1＝2，则该三棱柱的外接球的体积为()A．B．C．D．20π5．已知矩形ABCD中，AB＝2AD＝2，E，F分别为AB，CD的中点，将四边形AEFD沿EF折起，使二面角A－EF－C的大小为120°，则过A，B，C，D，E，F六点的球的表面积为()A．6πB．5πC．4πD．3π6．已知直三棱柱ABC－A1B1C1的6个顶点都在球O的表面上，若AB＝AC＝1，AA1＝2，∠BAC＝，则球O的体积为()A．B．3πC．D．8π7．有一个圆锥与一个圆柱的底面半径相等，此圆锥的母线与底面所成角为，若此圆柱的外接球的表面积是圆锥的侧面积的4倍，则此圆柱的高是其底面半径的A．倍B．2倍C．倍D．3倍8．正四棱柱中，，二面角的大小为，则该正四棱柱外接球的表面积为A．B．C．D．9．正四棱柱中，，，设四棱柱的外接球的球心为，动点在正方形的边上，射线交球的表面点，现点从点出发，沿着运动一次，则点经过的路径长为________．10．已知圆柱的上底面圆周经过正三棱锥的三条侧棱的中点，下底面圆心为此三棱锥底面中心．若三棱锥的高为该圆柱外接球半径的2倍，则该三棱锥的外接球与圆柱外接球的半径的比值为________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com