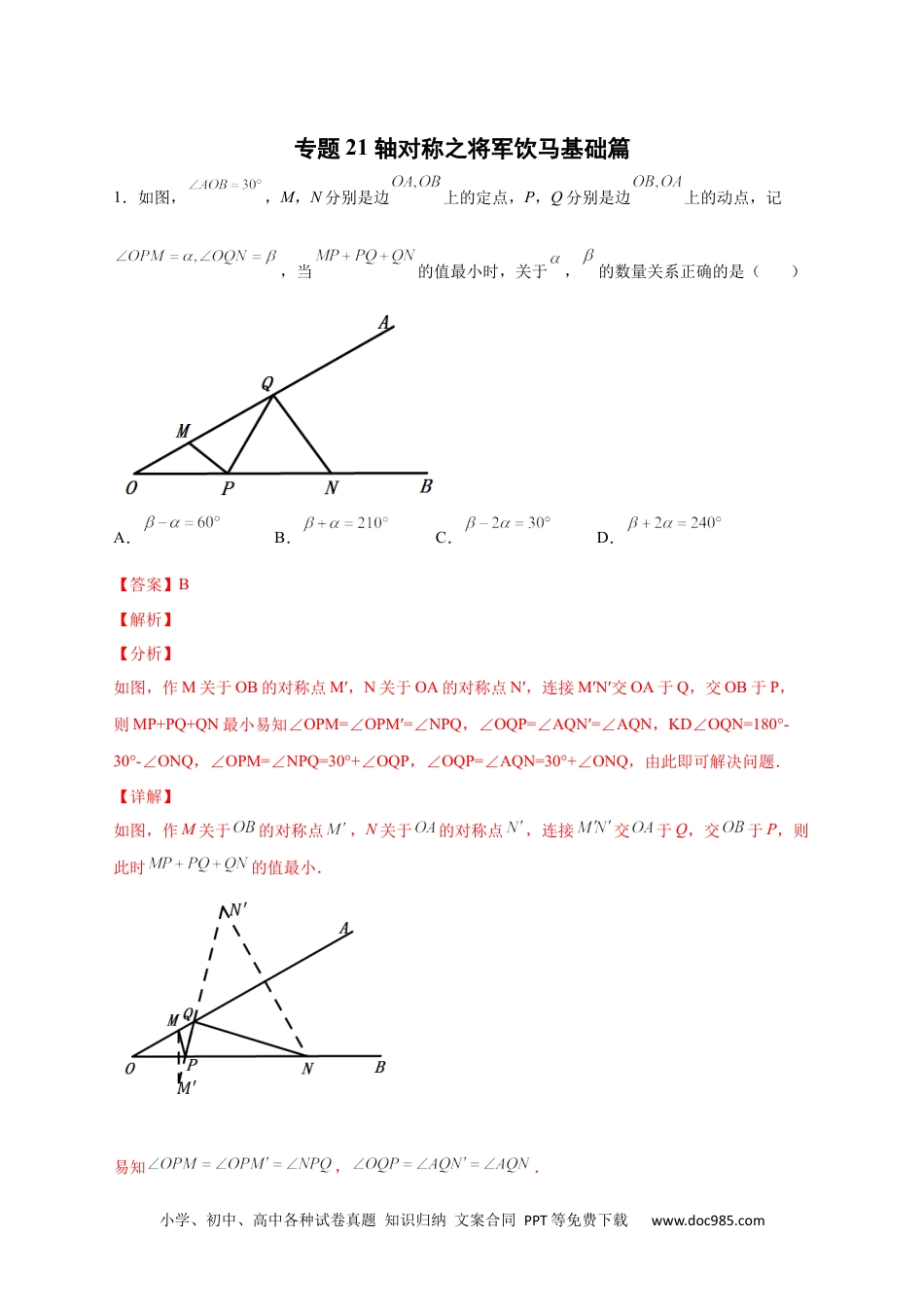
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题21轴对称之将军饮马基础篇1．如图，，M，N分别是边上的定点，P，Q分别是边上的动点，记，当的值最小时，关于，的数量关系正确的是（）A．B．C．D．【答案】B【解析】【分析】如图，作M关于OB的对称点M′，N关于OA的对称点N′，连接M′N′交OA于Q，交OB于P，则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ，∠OQP=∠AQN′=∠AQN，KD∠OQN=180°-30°-∠ONQ，∠OPM=∠NPQ=30°+∠OQP，∠OQP=∠AQN=30°+∠ONQ，由此即可解决问题．【详解】如图，作M关于的对称点，N关于的对称点，连接交于Q，交于P，则此时的值最小．易知，．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com ，，∴．故选：B.【点睛】本题考查轴对称-最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．2．如图，△ABC是等腰三角形，底边BC的长为4，面积是18，腰AC的垂直平分线EF分别交AC，AB于点E，F．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值是（）A．11B．13C．9D．8【答案】A【解析】【分析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CM+MD的最小值，由此即可得出结论．【详解】解：连接AD， △ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴，解得AD=9， EF是线段AC的垂直平分线，∴点C关于直线EF的对称点为点A，∴CM=AM，∴CD+CM+DM=CD+AM+DM， AM+DM≥AD，∴AD的长为CM+MD的最小值，∴△CDM的周长最短=（CM+MD）+CD=AD+BC=9+×4=9+2=11．故选：A．【点睛】本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．3．如图，，点M，N分别是边，上的定点，点P，Q分别是边，上的动点，记，，当的值最小时，的大小=__________（度）．【答案】50【解析】【分析】作M关于OB的对称点，N关于OA的对称点，连接，交OB于点P，交OA于点Q，连接MP，QN，可知此时最小，此时，再根据三角形外角的性质和平角的定义即小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com可得出结论．【详解】作M关于OB的对称点，N关于OA的对称点，连接，交OB于点P，交OA于点Q，连接MP，QN，如图所示．根据两点之间，线段最短，可知此时最小，即，∴， ，∴， ，，∴，∴．故答案为：50．【点睛】本题考查轴对称-最短问题、三角形内角和，三角形外角的性质等知识，灵活运用所学知识解决问题是解题的关键，综合性较强．4．如图，点是内任意一点，，点和点分别是射线和射线上的动点，，则周长的最小值是______．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】3【解析】【分析】根据“将军饮马”模型将最短路径问题转化为所学知识“两点之间线段最短”可找到周长的最小的位置，作出图示，充分利用对称性以及，对线段长度进行等量转化即可．【详解】解：如图所示，过点P分别作P点关于OB、OA边的对称点、，连接、、、、，其中分别交OB、OA于点N、M，根据“两点之间线段最短”可知，此时点M、N的位置是使得周长的最小的位置．由对称性可知：，，为等边三角形的周长===3故答案为：3小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【点睛】本题是典型的的最短路径问题，考查了最短路径中的“将军饮马”模型，能够熟练利用其原理“两点之间线段最短”作出最短路径示意图是解决本题的关键．5．如图，是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当的周长最小时，的度数为______．【答案】30°##30度【解析】【分析】连接BP，由等边三角形的性质可知AD为BC的垂直平分线，即得出BP=CP，由此可知要使△PCE的周长最小，即P点为BE与AD的交点时．最后根据等边三角形三线合一的性质，即得出CP平分，从而可求出．【...