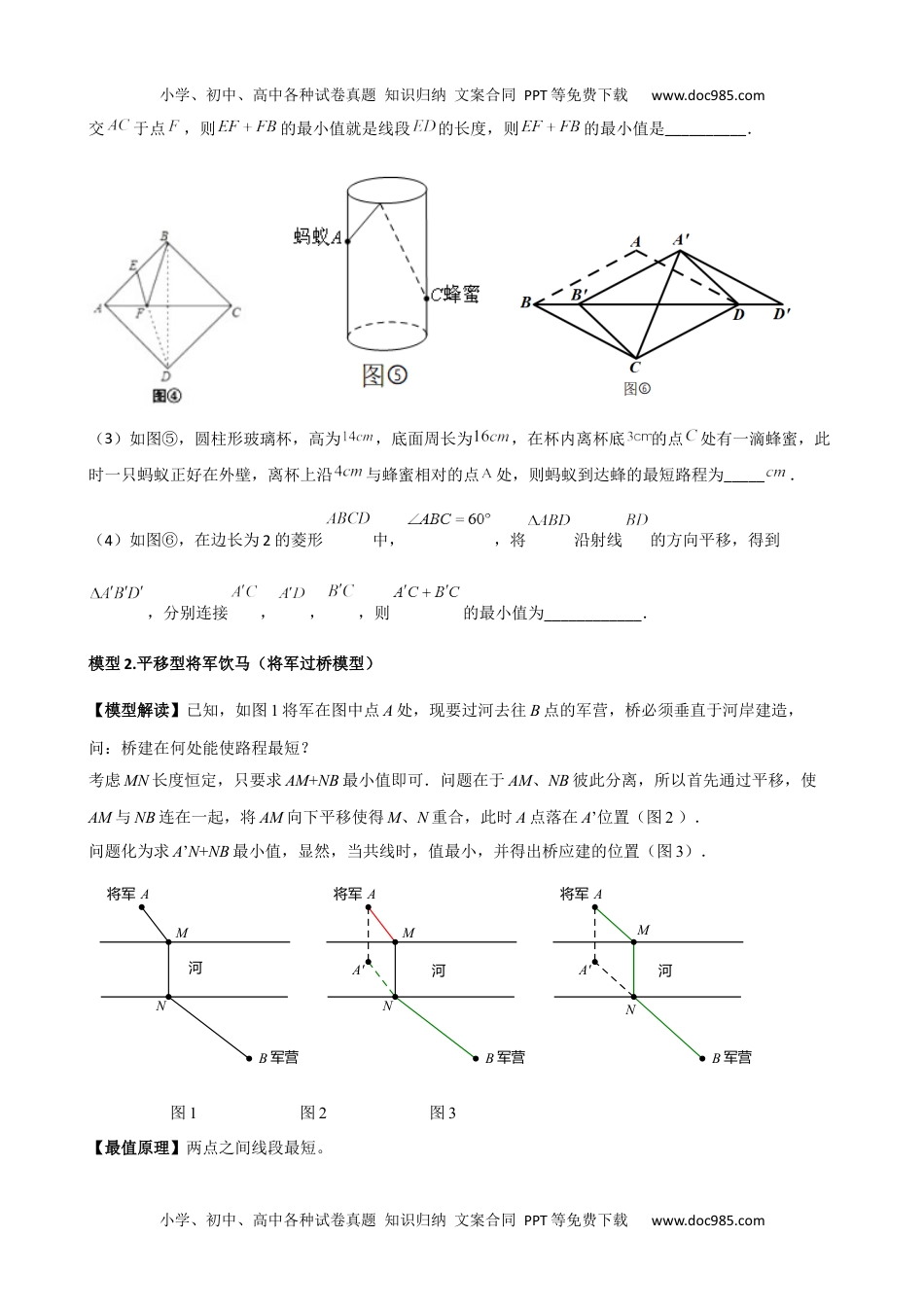
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题09最值模型---将军饮马最值问题在中考数学常以压轴题的形式考查,将军饮马问题是由轴对称衍生而来,同时还需掌握平移型将军饮马,主要考查转化与化归等的数学思想。在各类考试中都以中高档题为主,中考说明中曾多处涉及。本专题就最值模型中的将军饮马问题进行梳理及对应试题分析,方便掌握。在解决几何最值问题主要依据是:①两点之间,线段最短;②垂线段最短,涉及的基本方法还有:利用轴对称变换化归到“三角形两边之和大于第三边”、“三角形两边之差小于第三边”等。模型1.求两条线段和的最小值(将军饮马模型)【模型解读】在一条直线m上,求一点P,使PA+PB最小;(1)点A、B在直线m两侧:(2)点A、B在直线同侧:mABPmABmABPmABA'【最值原理】两点之间线段最短。上图中A’是A关于直线m的对称点。例1.(2022·湖南娄底·中考真题)菱形的边长为2,,点、分别是、上的动点,的最小值为______.例2.(2022·四川眉山·中考真题)如图,点为矩形的对角线上一动点,点为的中点,连接,,若,,则的最小值为________.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例3.(2022·贵州铜仁·中考真题)如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为________.例4.(2022·江苏南京·模拟预测)【模型介绍】古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营.他总是先去营,再到河边饮马,之后,再巡查营.如图①,他时常想,怎么走才能使每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.如图②,作点关于直线的对称点,连结与直线交于点,连接,则的和最小.请你在下列的阅读、理解、应用的过程中,完成解答.理由:如图③,在直线上另取任一点,连结,,, 直线是点,的对称轴,点,在上,(1)∴__________,_________,∴____________.在中, ,∴,即最小.【归纳总结】在解决上述问题的过程中,我们利用轴对称变换,把点在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即转化为“三角形两边之和大于第三边”的问题加以解决(其中点为与的交点,即,,三点共线).由此,可拓展为“求定直线上一动点与直线同侧两定点的距离和的最小值”问题的数学模型.【模型应用】(2)如图④,正方形的边长为4,为的中点,是上一动点.求的最小值.解析:解决这个问题,可借助上面的模型,由正方形对称性可知,点与关于直线对称,连结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com交于点,则的最小值就是线段的长度,则的最小值是__________.(3)如图⑤,圆柱形玻璃杯,高为,底面周长为,在杯内离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁到达蜂的最短路程为_____.(4)如图⑥,在边长为2的菱形中,,将沿射线的方向平移,得到,分别连接,,,则的最小值为____________.模型2.平移型将军饮马(将军过桥模型)【模型解读】已知,如图1将军在图中点A处,现要过河去往B点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?考虑MN长度恒定,只要求AM+NB最小值即可.问题在于AM、NB彼此分离,所以首先通过平移,使AM与NB连在一起,将AM向下平移使得M、N重合,此时A点落在A’位置(图2).问题化为求A’N+NB最小值,显然,当共线时,值最小,并得出桥应建的位置(图3).河B军营A将军NMA'河B军营A将军NMA'河B军营A将军NM图1图2图3【最值原理】两点之间线段最短。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985....