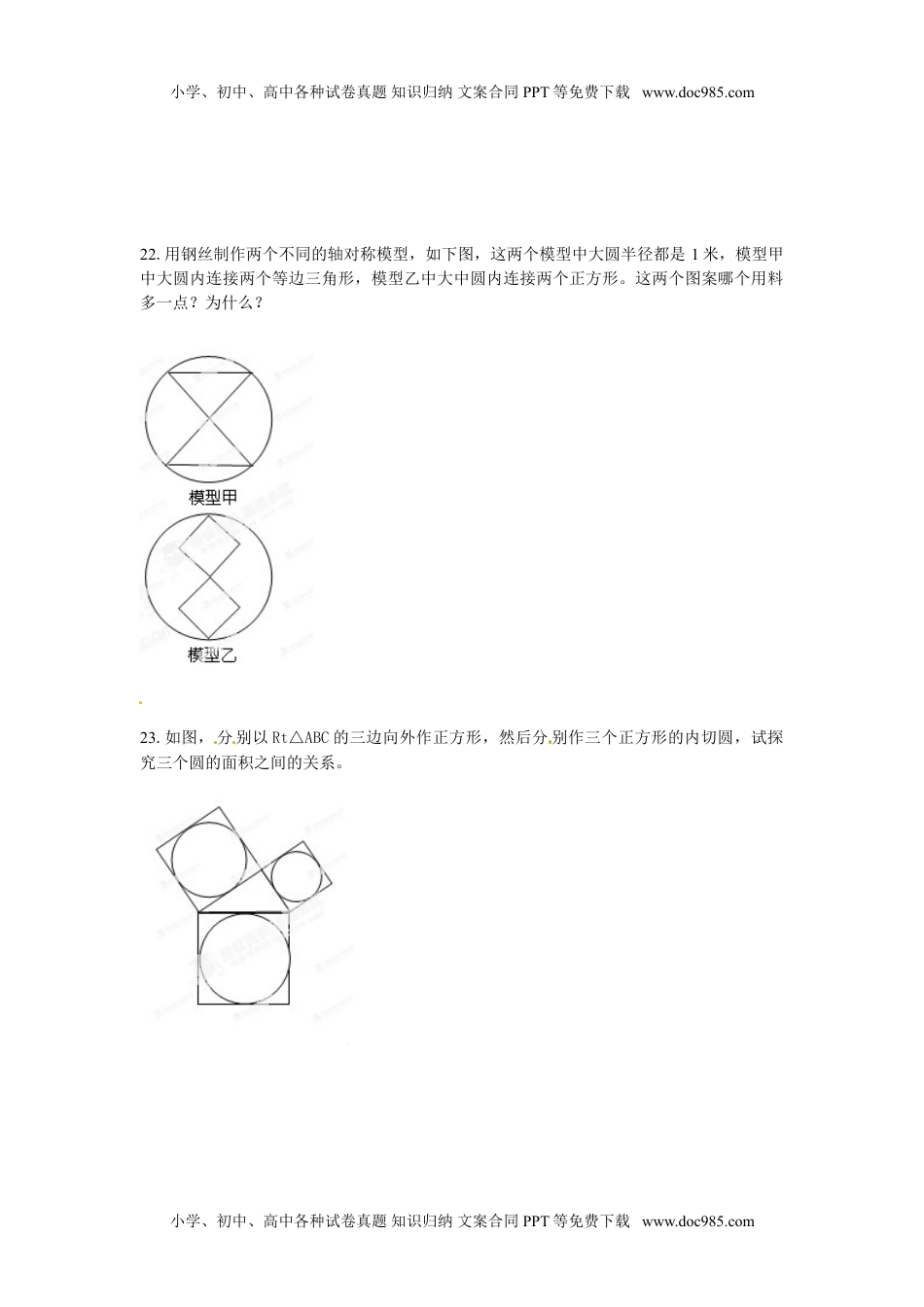
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第二章圆复习(时间：120分钟，满分：120分)一、选择题：（每小题3分，共36分）1.⊙O的直径是15㎝，CD经过圆心O，与⊙O交于C、D两点，垂直弦AB于M，且OM：OC=3：5，则AB=（）A．24㎝B．12㎝C．6㎝D．3㎝2.⊙O的直径是3，直线与⊙O相交，圆心O到直线的距离是d，则d应满足（）A．d>3B．1.5<d<3C．0≤d<1.5D．0<d<33.半径为1的⊙O中，120º的圆心角所对的弧长是（）A．B．C．D．4.若直径为4㎝，6㎝的两个圆相外切，那么与这两个圆都相切且半径为5㎝的圆的个数是（）A．5个B．4个C．3个D．2个5.圆内接正方形与该圆的内接正六边形的周长比为（）A．2：3B．：C．：2D．2：36、已知O为△ABC的外心，∠A＝60°，则∠BOC的度数是（）A．30ºB．60ºC．90ºD．120º7.下列命题中正确的是()A．三点确定一个圆B．在同圆中，同弧所对的圆周角相等C．平分弦的直线垂直于弦D．相等的圆心角所对的弧相等8.如图，已知圆心角∠AOB的度数为100°，则圆周角∠ACB的度数是()A．80°B．100°C．120°D．130°C9.下列图形中,既是轴对称又是中心对称的图形是()A．平行四边形B．等腰梯形C．等边三角形D．圆10.如图，⊙O1与⊙O2是两枚同样大的硬币，其中一个固定，另一个沿其周围滚动，两枚硬币总是保持有一点相接触(相外切)．当滚动的硬币沿固[来源:学*科*网]定的硬币周围滚动一圈，回到原来位置时,滚动的那个硬币自转的周数为()[来源:学科网ZXXK]A．1B．2小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．3D．411、如图，PA为⊙O的切线，A为切点，PO交⊙O于点B.。PA=4，OA=3，则cos∠APO的值为（）A．B．C．D．[来源:学科网ZXXK]12、已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的大小是（）A70°B40°C50°D20°二、填空题(每小题3分,共30分)11．与已知点A的距离为3cm的点所组成的平面图形是．12.⊙O的直径是8cm，P为⊙O内一点，PO=2cm，过点P最短的弦AB=,13.已知AB是⊙O直径，D是圆上任意一点[来源:学+科+网Z+X+X+K](不与A、B重合)，连结BD，并延长到C，使DC=DB,连结AC,则△ABC的形状是三角形.14.一条弦把圆分为2：3的两部分，那么这条弦所对的圆周角的度数为.15.如图,CA为⊙O的切线，切点为A，点B在⊙O上，如果16.过⊙O内一点P的最长的弦是10㎝，最短的弦是8㎝，则OP和长为㎝。17.如图弦AC，BD相交于E，并且,∠BEC=110°,则∠ACD的度数是。18.若三角形的周长为P，面积为S，其内切圆的半径为r,则r：S=m]19.已知∠AOB=30°，M为OB边上一点，以M为圆心，2㎝为半径作⊙M与OA相切，切点为N，则△MON的面积为。20.如图①是半径为1的圆，在其中挖去2个半径为的圆得到图②，挖去22个半径为（）2的圆得到图③……，则第n(n>1)个图形阴影部分的面积是。三、解答题：（每小题8分，共40分）21.如图，AB是⊙O的直径，CF⊥AB交⊙O于E、F，连结AC交⊙O于D。求证：CD·AD=DE·DF。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comABCDE第7题AFBECDO·小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com22.用钢丝制作两个不同的轴对称模型，如下图，这两个模型中大圆半径都是1米，模型甲中大圆内连接两个等边三角形，模型乙中大中圆内连接两个正方形。这两个图案哪个用料多一点？为什么？23.如图，分别以Rt△ABC的三边向外作正方形，然后分别作三个正方形的内切圆，试探究三个圆的面积之间的关系。[来源:Z+xx+k.Com]小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com[来源:学§科§网]24.如图，在直角坐标系中，点A在x轴负半轴上，点B在x轴正半轴上，以线段AB为弦的⊙C与直线x=-2相切于点E（-2，），交x轴于点D，线段AE的长为.求点A、B的坐标。25.如图，四边形ABCD内接于圆，若AB=AC，且∠ABD=60°.求证：AB=BD+CD。[来源:学+科+网Z+X+X+K]小学、初中、高中各种...