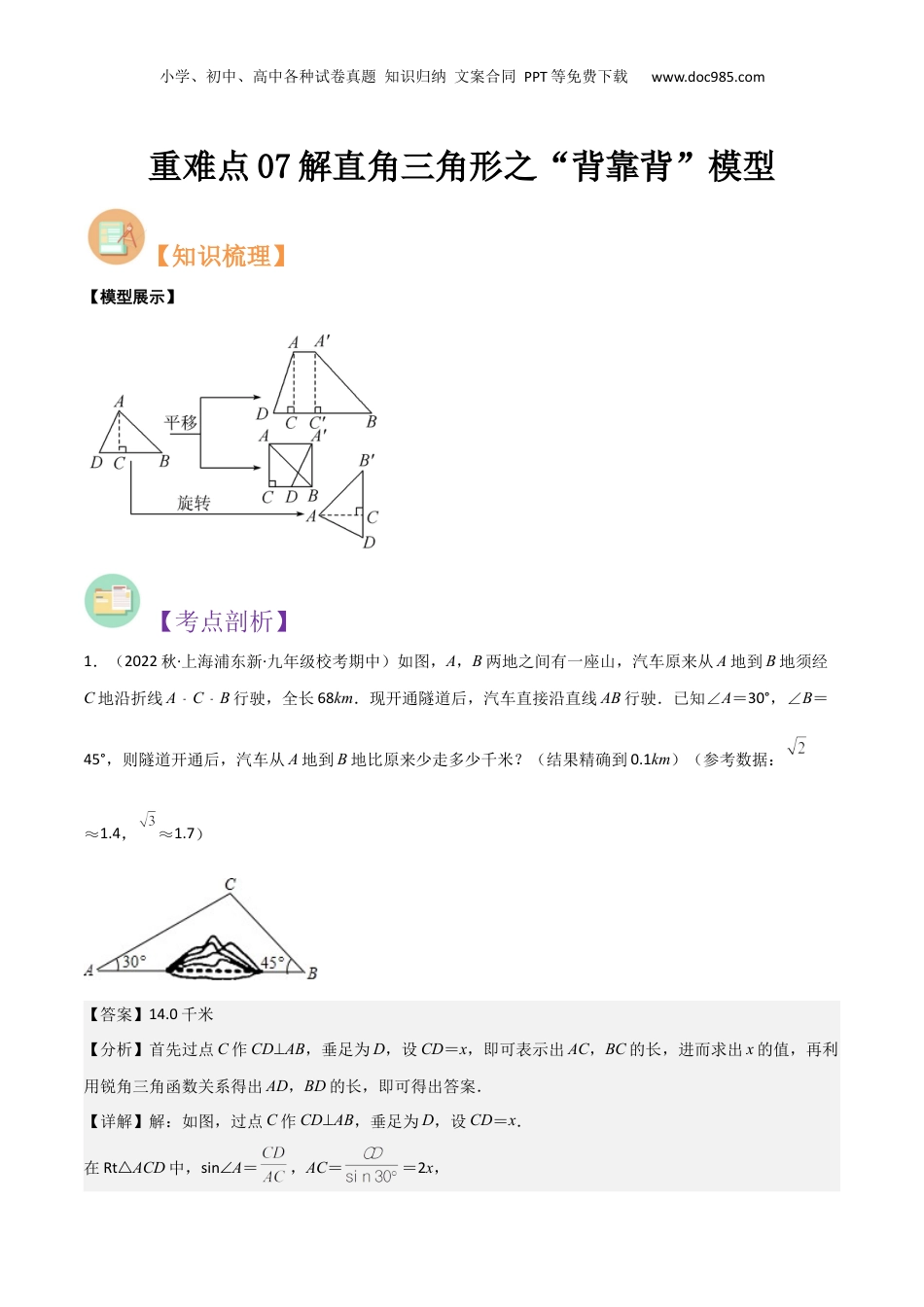
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点07解直角三角形之“背靠背”模型【知识梳理】【模型展示】【考点剖析】1．（2022秋·上海浦东新·九年级校考期中）如图，A，B两地之间有一座山，汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶，全长68km．现开通隧道后，汽车直接沿直线AB行驶．已知∠A＝30°，∠B＝45°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果精确到0.1km）（参考数据：≈1.4，≈1.7）【答案】14.0千米【分析】首先过点C作CD⊥AB，垂足为D，设CD＝x，即可表示出AC，BC的长，进而求出x的值，再利用锐角三角函数关系得出AD，BD的长，即可得出答案．【详解】解：如图，过点C作CD⊥AB，垂足为D，设CD＝x．在Rt△ACD中，sin∠A＝，AC＝＝2x，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在Rt△BCD中，sin∠B＝，BC＝＝x， AC+BC＝2x+x＝68，∴x＝，在Rt△ACD中，tan∠A＝，AD＝，在Rt△BCD中，tan∠B＝，BD＝＝20，AB＝20+20≈54，AC+BC﹣AB＝6854﹣＝14.0（km）．答：隧道开通后，汽车从A地到B地比原来少走14.0千米．【点睛】本题主要考查了解直角三角形的实际应用，准确分析计算是解题的关键．2．（2023·上海·一模）如图，C地在A地的正东方向，因有大山阻隔，由A地到C地需要绕行B地，已知B位于A地北偏东67°方向，距离A地520km，C地位于B地南偏东30°方向，若打通穿山隧道，建成两地直达高铁，求A地到C地之间高铁线路的长．（结果保留整数）参考数据：（sin67°≈；cos67°≈；tan67°≈；≈1.73）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】地到地之间高铁线路的长约为．【分析】过点B作BDAC⊥于点D，利用锐角三角函数的定义求出AD及CD的长，进而可得出结论．【详解】解：如解图，过点作于点， 地位于地北偏东方向，距离地，∴，∴，． 地位于地南偏东方向，∴，∴，∴．答：地到地之间高铁线路的长约为．【点睛】本题考查的是解直角三角形的应用-方向角问题，解题关键是添加常用辅助线，构造直角三角形．3．（2020·上海杨浦·统考一模）如图，为了测量河宽，在河的一边沿岸选取B、C两点，对岸岸边有一块石头A，在中，测得，，米，求河宽（即点A到边的距离）（结果精确到0.1米）．（参考数据：，，，）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】河宽约为33.6米【分析】过A作AD⊥BC于D，并设AD=x米，则由已知条件可以得到关于x的方程，解方程即可得到河的宽度．【详解】解：如图，过A作AD⊥BC于D，并设AD=x米， ∠C=45°，∴∠DAC=90°-45°=45°，∴CD=AD=x， ∠B=64°，∴BD=， BC=50米，∴，解之得：x≈33.6，答：河宽约33.6米．【点睛】本题考查解直角三角形的应用，熟练掌握锐角三角函数的定义并结合方程思想求解是解题关键．4．（2023·上海·一模）如图，在港口A的南偏东37°方向的海面上，有一巡逻艇B，A、B相距20海里，这时在巡逻艇的正北方向及港口A的北偏东67°方向上，有一渔船C发生故障．得知这一情况后，巡逻艇以25海里/小时的速度前往救援，问巡逻艇能否在1小时内到达渔船C处？（参考数据：，，，，，）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】巡逻艇能在1小时内到达渔船C处【分析】由已知可得在△ABC中，∠C＝67°，∠B＝37°，且AB＝20海里，要求BC的长，可以过A作AD⊥BC于D，分别求出CD和BD的长，就可转化为运用三角函数解直角三角形．【详解】解答：过点A作AH⊥BC，垂足为点H．由题意，得∠ACH＝67°，∠B＝37°，AB＝20．在Rt△ABH中， ，，∴，，在Rt△ACH中， ，∴，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴BC＝BH＋CH≈16＋5＝21，21÷25 ＜1，∴巡逻艇能在1小时内到达渔船C处．【点睛】本题考查了解直角三角形的应用，解答本题的关键是将一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．【过关检测】1．（2020·内蒙古赤峰·统考中考真题）如图，航拍无...