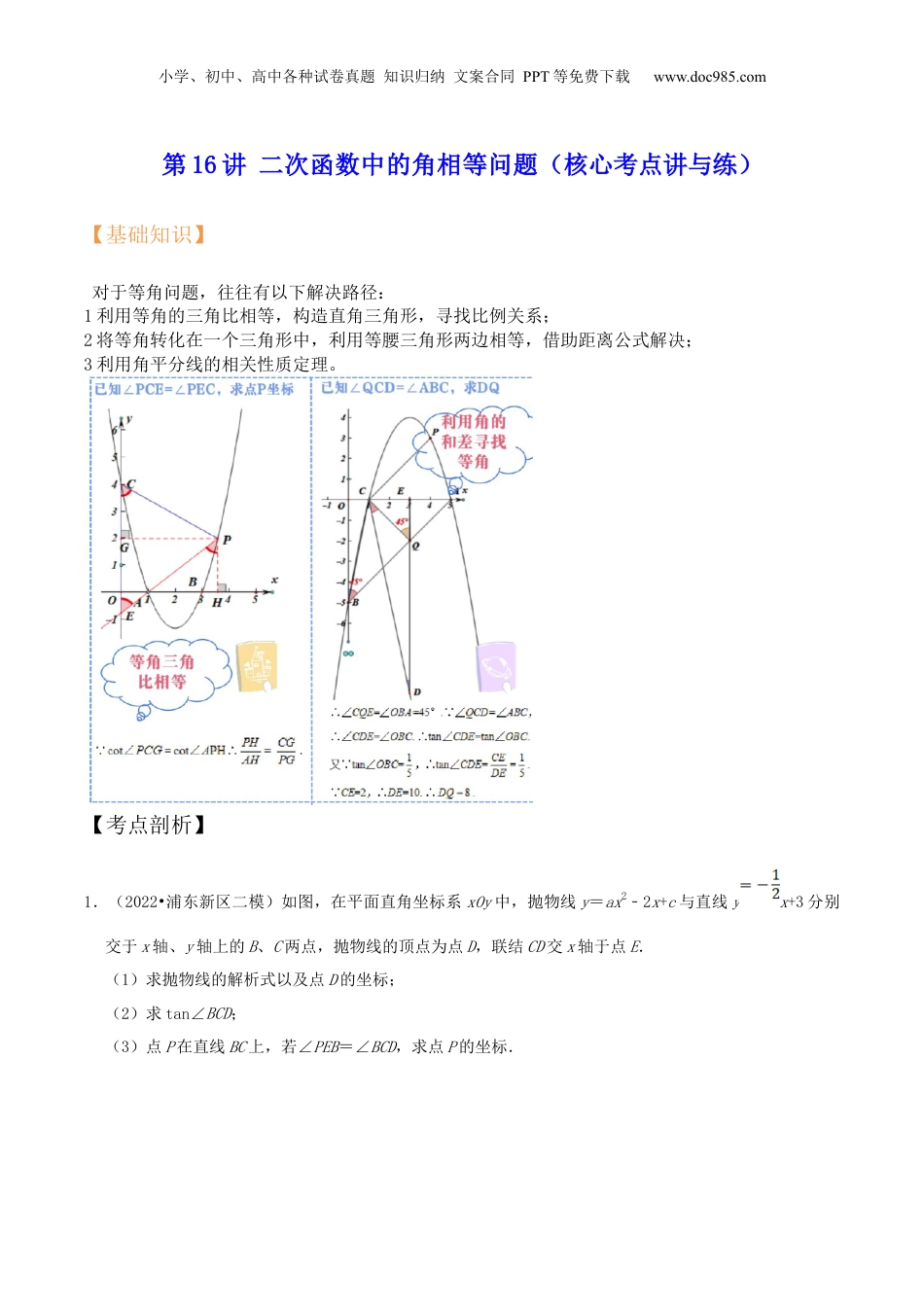
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第16讲二次函数中的角相等问题（核心考点讲与练）【基础知识】对于等角问题，往往有以下解决路径：1利用等角的三角比相等，构造直角三角形，寻找比例关系；2将等角转化在一个三角形中，利用等腰三角形两边相等，借助距离公式解决；3利用角平分线的相关性质定理。【考点剖析】1．（2022•浦东新区二模）如图，在平面直角坐标系xOy中，抛物线y＝ax2﹣2x+c与直线yx+3分别交于x轴、y轴上的B、C两点，抛物线的顶点为点D，联结CD交x轴于点E．（1）求抛物线的解析式以及点D的坐标；（2）求tan∠BCD；（3）点P在直线BC上，若∠PEB＝∠BCD，求点P的坐标．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】（1）直接利用待定系数法求出二次函数解析式进而得出答案；（2）利用锐角三角函数关系得出EC，BF的长，进而得出答案；（3）分别利用①点P在x轴上方，②点P在x轴下方，分别得出点P的坐标．【解答】解：（1）由题意得B（6，0），C（0，3），把B（6，0）C（0，3）代入y＝ax2﹣2x+c得，解得：，∴抛物线的解析式为：yx2﹣2x+3（x2﹣8x）+3（x﹣4）2﹣1，∴D（4，﹣1）；（2）可得点E（3，0），OE＝OC＝3，∠OEC＝45°，过点B作BF⊥CD，垂足为点F小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在Rt△OEC中，EC3，在Rt△BEF中，BF＝BE•sin∠BEF，同理，EF，∴CF＝3，在Rt△CBF中，tan∠BCD；（3）设点P（m，） ∠PEB＝∠BCD，∴tan∠PEB＝tan∠BCD，①点P在x轴上方∴，解得：，∴点P（，），②点P在x轴下方∴，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解得：m＝12，∴点P（12，﹣3），综上所述，点P（，）或（12，﹣3）．【点评】此题主要考查了二次函数的综合以及锐角三角函数关系的应用，正确分类讨论是解题关键．2．（2022春•静安区期中）在平面直角坐标系中，已知抛物线与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3），对称轴为直线x＝1，交x轴于点E．（1）求该抛物线的表达式；（2）点D为此抛物线的顶点，证明：∠CDB＝∠CAB；（3）在x轴上是否存在一点M，以及抛物线上一点N，使得以M、N、B、C四点构成的四边形为平行四边形？如果有，请直接写出点M的坐标；如果没有，请说明理由．【分析】（1）用待定系数法求解即可；（2）根据题意求出线段CD，BC，BD的长度，证明ABDC是直角三角形，再求出两个角对应的正切值，从而证明两个角相等；（3）按照对边平行进行讨论，根据对边相等或者对角线互相平分进行计算，也可结合图象判断．【解答】（1）解：设抛物线解析式为y＝ax2+bx+c（a≠0），小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com 抛物线经过点A（﹣1，0），C（0，3），且对称轴为直线x＝1，∴，解得，∴抛物线的表达式为y＝﹣x2+2x+3；（2）证明令y＝0，则﹣x2+2x+3＝0，解得：x1＝﹣1，x2＝3，∴B（3，0）， y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴顶点D坐标（1，4），∴CD，BD2，CB3， BC2+CD2＝（3）2+（）2＝20，BD2＝（2）2＝20，∴BC2+CD2＝BD2，∴∠BCD＝90°，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴∠tan∠CDB3， tan∠CAB3，∴∠CDB＝∠CAB；（3）解：①当BM∥CN时，如图： 对称轴为直线x＝1，C（0，3），∴N（2.3），CN＝2， B（3，0），∴CN＝BM，∴BM＝2，当M点在B点左侧时，M1（1，0），当M点在B点右侧时，M2（5，0），∴M1（1，0）或M2（5，0）；②当CM∥BN时，如图：CN与BM互相平分，N点和C点纵坐标互为相反数，可得N点纵坐标为﹣3，把y＝﹣3代入解析式得：﹣x2+2x+3﹣3，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com解得：x11，x21，所以N1的横坐标为1．，N2的横坐标为1，由平行四边形对角线互相平分可得1+0＝3+xM或1+0＝3+xM，解得xN2或xN2，所以M3（2，0）或M4（2，0）．综上所述：M1（1，0）或M2（5，0）或M3（2，0）或M4（2，0）．【点评】本题主要考查了二次函数的综合题，用待定...