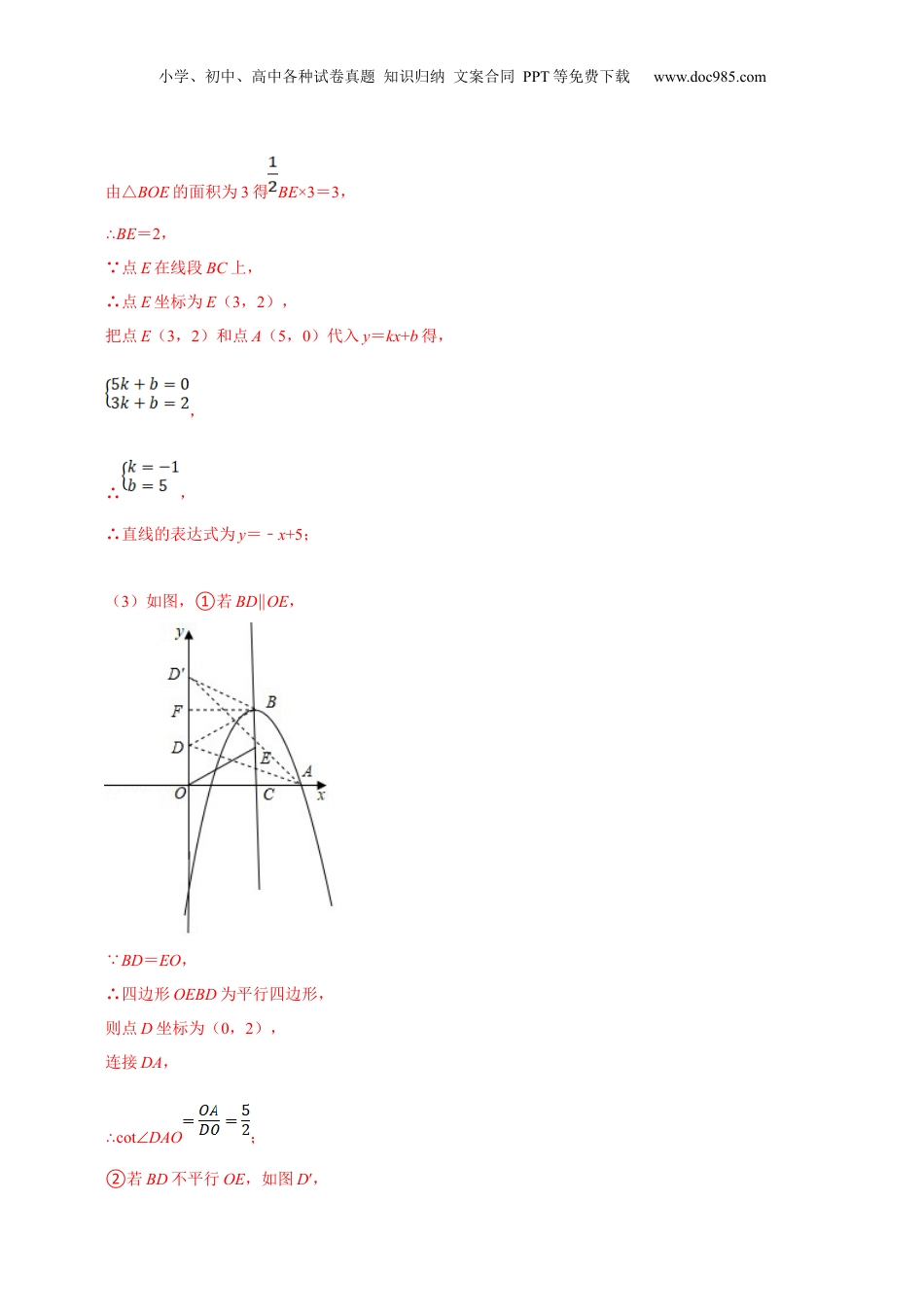
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第18讲二次函数中的线段相等与和差倍半问题（核心考点讲与练）【考点剖析】1．（2022•黄浦区二模）在平面直角坐标系xOy中，抛物线y＝﹣x2+mx+n经过点A（5，0），顶点为点B，对称轴为直线x＝3，且对称轴与x轴交于点C．直线y＝kx+b经过点A，与线段BC交于点E．（1）求抛物线y＝﹣x2+mx+n的表达式；（2）联结BO、EO．当△BOE的面积为3时，求直线y＝kx+b的表达式；（3）在（2）的条件下，设点D为y轴上的一点，联结BD、AD．当BD＝EO时，求∠DAO的余切值．【分析】（1）利用待定系数法和抛物线对称轴公式即可求解；（2）先求出顶点B坐标，根据△BOE的面积为3求出BE，进而求出点E坐标，利用待定系数法即可求解；（3）分BD∥OE和BD与OE不平行两种情况，分别求出D坐标，利用余切定义即可求解．【解答】解：（1） 抛物线y＝﹣x2+mx+n经过点A（5，0），对称轴为直线x＝3，∴，∴，∴抛物线表达式为y＝﹣x2+6x5﹣；（2）把x＝3代入y＝﹣x2+6x5﹣得y＝4，∴抛物线顶点B坐标为（3，4），小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com由△BOE的面积为3得BE×3＝3，∴BE＝2， 点E在线段BC上，∴点E坐标为E（3，2），把点E（3，2）和点A（5，0）代入y＝kx+b得，，∴，∴直线的表达式为y＝﹣x+5；（3）如图，①若BD∥OE， BD＝EO，∴四边形OEBD为平行四边形，则点D坐标为（0，2），连接DA，cot∴∠DAO；②若BD不平行OE，如图D′，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则四边形OEBD′为等腰梯形，做BF⊥y轴于F，则D′F＝DF＝2，∴点D′坐标为（0，6），连接D′A，cot∴∠D′AO，综上所述，此时∠DAO的余切值为或．【点评】本题为二次函数综合题，考查了二次函数性质，求一次函数解析式，余切定义等知识，熟练掌握各知识点是解题关键，解第（3）步时要注意分类讨论思想应用．2.（2021闵行区二模24）（12分）在平面直角坐标系xOy中，抛物线y＝﹣x2+mx+n经过点A（5，0），顶点为点B，对称轴为直线x＝3，且对称轴与x轴交于点C．直线y＝kx+b，经过点A，与线段BC交于点E．（1）求抛物线y＝﹣x2+mx+n的表达式；（2）联结BO、EO．当△BOE的面积为3时，求直线y＝kx+b的表达式；（3）在（2）的条件下，设点D为y轴上的一点，联结BD、AD，当BD＝EO时，求∠DAO的余切值．【分析】（1）利用待定系数法和抛物线对称轴公式即可求解；（2）先求出顶点B坐标，根据△BOE的面积为3求出BE，进而求出点E坐标，利用待定系数法即可求解；（3）分BD∥OE和BD与OE不平行两种情况，分别求出D坐标，利用余切定义即可求解．【解答】解：（1） 抛物线y＝﹣x2+mx+n经过点A（5，3），∴，∴，∴抛物线表达式为y＝﹣x2+6x6﹣；（2）把x＝3代入y＝﹣x2+2x5﹣得y＝4，∴抛物线顶点B坐标为（5，4），由△BOE的面积为3得BE×3＝3，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴BE＝2， 点E在线段BC上，∴点E坐标为E（3，3），把点E（3，2）和点A（8，，∴，∴直线表达式为y＝﹣x+5；（3）如图，①若BD∥OE，则四边形OEBD1为平行四边形，则点D4坐标为（0，2），连接D5A，cot∴∠D1AO＝＝，综上所述，此时∠DAO的余切值为或．【点评】本题为二次函数综合题，考查了二次函数性质，求一次函数解析式，余切定义等知识，熟练掌握各知识点是解题关键，解第（3）步时要注意分类讨论思想应用．3．（2022春•徐汇区校级期中）如图，二次函数yx2+bx+2的图象与x轴交于A、B两点，与y轴相交小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com于点C，点A的坐标为（﹣4，0），P是抛物线上一点（点P与点A、B、C都不重合）．（1）求抛物线解析式；（2）求点B的坐标；（3）设直线PB与直线AC相交于点M，且存在这样的点P，使得PM：MB＝1：2，试确定点P的横坐标．【分析】（1）由点A的坐标，利用二次函数图象上点的坐标特征可求出b的值，即可得到抛物线的解析式；（2）代入y＝0求出x值，可得出点B的坐标；（3）（解法一）代入x＝0求出y值，进而可得出点C的坐...