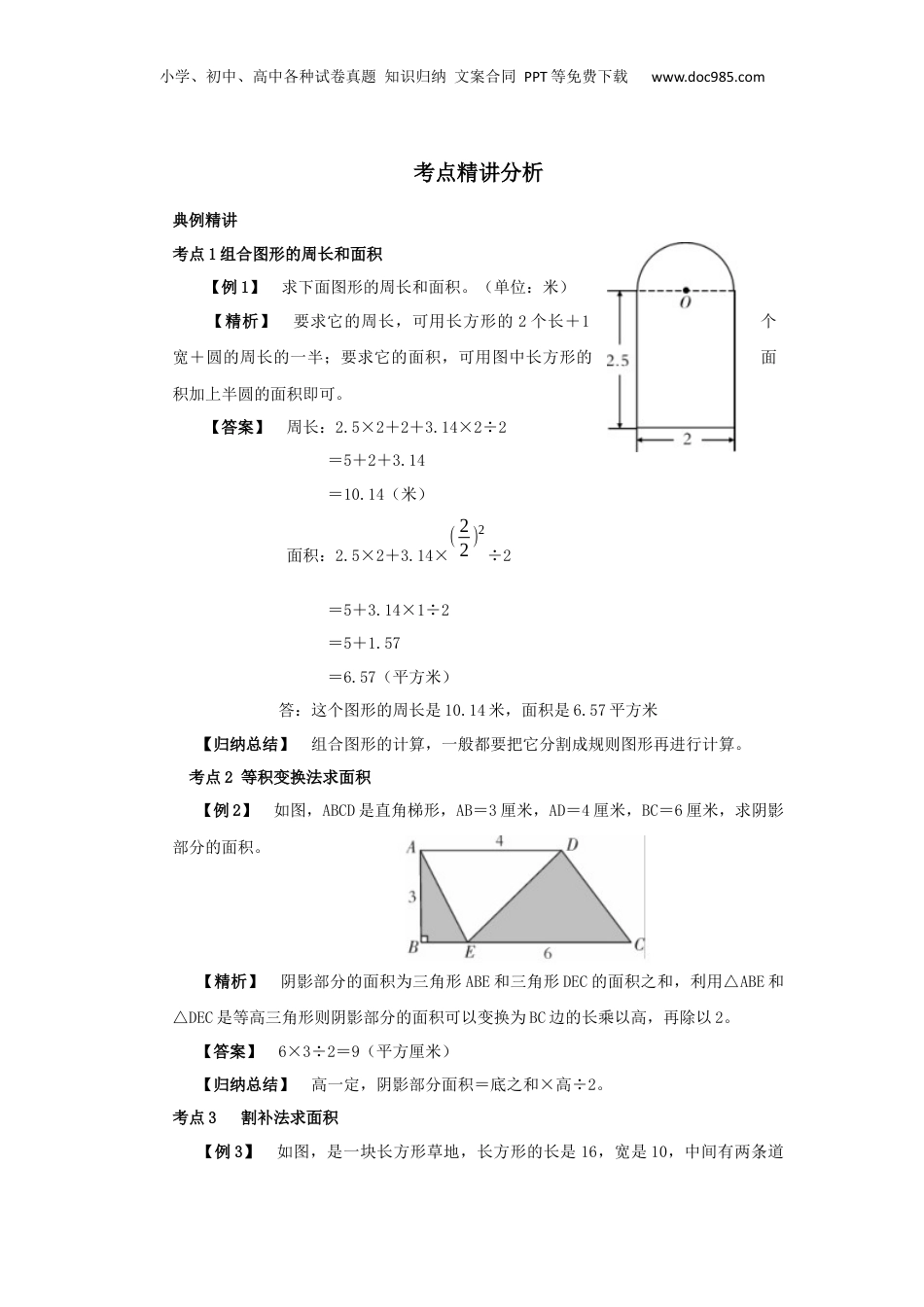
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com23.平面图形的测量知识要点梳理一、基本图形周长面积计算公式二、组合图形求周长、面积1．阴影面积＝整体－空白2．代换法梯形中的蝴蝶定理：①S1＝S4②S1×S3＝S2×S43．分割法4．等高三角形（1）等高三角形面积的比等于底之比。（2）等高三角形的常用判定方法：有一个公用的顶点，其余顶点均在同一直线上，所有顶点均在同一对平行线上。（3）等底三角形的面积之比等于高之比。5.交叉定理ad=bc扇形r表示半径α表示圆心角S=πr2×α360°C=2πr×α360°圆环r表示小圆半径R表示大圆半径圆环面积=大圆面积-小圆面积S环=π(R2−r2)abcd小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com考点精讲分析典例精讲考点1组合图形的周长和面积【例1】求下面图形的周长和面积。（单位：米）【精析】要求它的周长，可用长方形的2个长＋1个宽＋圆的周长的一半；要求它的面积，可用图中长方形的面积加上半圆的面积即可。【答案】周长：2.5×2＋2＋3.14×2÷2＝5＋2＋3.14＝10.14（米）面积：2.5×2＋3.14×(22)2÷2＝5＋3.14×1÷2＝5＋1.57＝6.57（平方米）答：这个图形的周长是10.14米，面积是6.57平方米【归纳总结】组合图形的计算，一般都要把它分割成规则图形再进行计算。考点2等积变换法求面积【例2】如图，ABCD是直角梯形，AB＝3厘米，AD＝4厘米，BC＝6厘米，求阴影部分的面积。【精析】阴影部分的面积为三角形ABE和三角形DEC的面积之和，利用△ABE和△DEC是等高三角形则阴影部分的面积可以变换为BC边的长乘以高，再除以2。【答案】6×3÷2＝9（平方厘米）【归纳总结】高一定，阴影部分面积＝底之和×高÷2。考点3割补法求面积【例3】如图，是一块长方形草地，长方形的长是16，宽是10，中间有两条道小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com路，一条是长方形，一条是平行四边形，那么，阴影部分的面积是多大？【精析】如果按常规解法，此题较麻烦，如果用割补法、平移法则较简单。把左边沿路这一块割下补在右边变成一个平行四边形，然后两条路平移到边上（如下图），就容易解答了。【答案】（16－2）×（10－2）＝14×8＝112（平方米）答：有草部分的面积为112平方米。考点4转化法求面积【例4】如图，正方形ABCD的边长为5cm，又△CEF的面积比△ADF的面积大5cm2，求CE的长。【精析】因为△CEF的面积比△ADF的面积大5平方厘米，这两个三角形分别加上公共部分则三角形ABE的面积比正方形ABCD的面积大5平方厘米，于是利用三角形和正方形的面积公式即可求解。【答案】（5×5＋5）×2÷5－5＝7cm【归纳总结】巧用等式的基本性质将局部转化为整体求面积。考点5辅助线法求面积【例5】如图所示的大正方形的边长是10厘米，求阴影部分的面积。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【精析】（辅助线法）如图所示：三角形BCF和三角形DCF等底等高（底和高分别等于大、小正方形的边长），则二者的面积相等，分别去掉公共部分（三角形CFH），那么剩余的部分的面积，仍然相等，即三角形BCH和三角形HFD的面积相等，于是阴影部分的面积就变成了大正方形的面积的一半，据此代入数据即可求解。【答案】10×10÷2＝100÷2＝50（平方厘米）答：三角形BFD的面积为50平方厘米。【归纳总结】解答此题的关键是：推论得出阴影部分的面积等于大正方形的面积的一半，问题即可得解。考点6平移法求面积【例6】如图，是由一个圆和两个正方形组成的图形，其中圆的半径为2，则图中阴影部分的面积为多少？【精析】将图中的阴影部分不规则图形的面积通过平移转化成规则图形的面积集中求解。【答案】2×2=44×4÷2-4×4÷4=4答：阴影部分的面积为4。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com名题精析【例】（西安某铁一中入学）右图是由4个边长为4厘米的正方形组成的图形，每个小正方形的一个顶点恰好在另一个正方形的中心，且边互相平行，则此图形的周长为（）cm，面积为（）cm2。【精析】根据图形可以看出组合图形中第一...