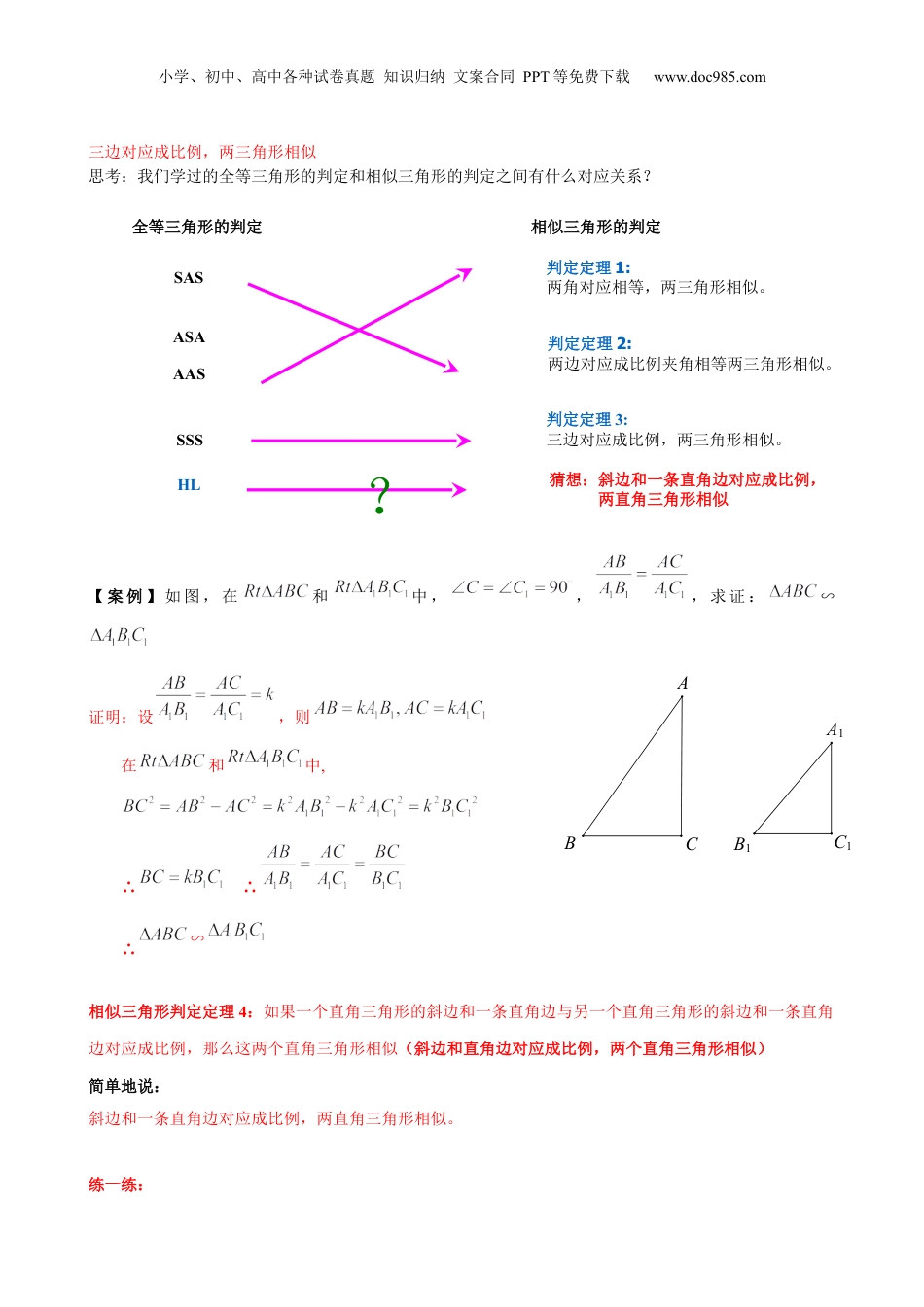
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第5讲直角三角形相似判定知识归纳思考：我们学过的三角形相似的判定定理有哪些？参考答案：预备定理：平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似。判定定理1：两角对应相等，两三角形相似。判定定理2：两边对应成比例且夹角相等，两三角形相似。判定定理3：三边对应成比例，两三角形相似。思考：RtΔABC和RtΔA'B'C'中，∠C＝∠C'＝90°．依据下列各组条件判定这两个三角形是不是相似，并说明为什么：(1)∠A＝25°，∠B'＝65°；(2)AC=3，BC＝4，A'C'＝6，B'C'＝8；(3)AB＝10，AC＝8，A'B'＝15，B'C'＝9．参考答案：（1）两角对应相等，两三角形相似（2）两边对应成比例且夹角相等，两三角形相似（3）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com三边对应成比例，两三角形相似思考：我们学过的全等三角形的判定和相似三角形的判定之间有什么对应关系？【案例】如图，在和中，，，求证：∽证明：设，则在和中,∴∴∴∽相似三角形判定定理4：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似（斜边和直角边对应成比例，两个直角三角形相似）简单地说：斜边和一条直角边对应成比例，两直角三角形相似。练一练：判定定理3:三边对应成比例，两三角形相似。判定定理1:两角对应相等，两三角形相似。SASASAAASSSSHL全等三角形的判定相似三角形的判定？猜想：斜边和一条直角边对应成比例，两直角三角形相似判定定理2:两边对应成比例夹角相等两三角形相似。C1B1ABCA1小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com一个直角三角形的两边长分别为3和6，另一个直角三角形的两边长分别为2和4，那么这两个直角三角形____相似．(填“一定”、“不一定”或“一定不”).参考答案：不一定试一试：如图，在△中，，垂足为，那么下列结论错误的是（）．；．；．；．．参考答案：B典型例题例1：如图，已知∠ABC=∠CDB=90°，AC=b，BC=a，当BD与a，b之间满足怎样的关系时，ΔABCΔ∽CDB?参考答案： ∴当时，即时∴∴当时，变式练习：在ΔABC与ΔBCD中，已知∠ABC=∠CDB=90°，AC=a，BC=b，当BD与a，b之间满足怎样的关系时，有两个三角形相似？参考答案：DCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com如图（1） ∴当时，即时∴∴当时，如图（2） ∴当时，即时∴所以当或时，有两个三角形相似注意：对条件探索性问题，在解题时应分类对每一种情况进行讨论，切不可凭主观想象，只解一种情况，而忽略其他的解。例题2：如图，在RtΔABC中，CD是斜边AB上的高，E是BC上的一点，AE交CD于点F，AE•AD＝AF•AC求证：(1)AE是∠CAB的平分线；(2)AB•AF＝AC•AE.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com参考答案：要证明AE是∠CAB的平分线，只要证明RtΔACE∽RtΔADF即可；要证明AB•AF＝AC•AE，只要证明ΔACFΔ∽ABE例题3：如图，在RtΔABC中，∠C=90°，CD是AB边上的高。求证：(1)(2)(3)能否根据（2）证明勾股定理？参考答案：（1）证明△ACD与△BCD相似；（2）证明△BCD与△ABC相似、证明△ACD与△ABC相似；（3）略课上习题1.已知在中，垂足为分别为垂足求证教法指导：引导学生推出射影定理，从而求出结果参考答案证明：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2.如图，在△ABC中，∠ACB=90°，CD是斜边AB上的高，G是DC延长线上一点，过B作BE⊥AG，垂足为E，交CD于点F．求证：CD2＝DF·DG．教法指导：用三点定形法确定两个三角形，然后通过三角形相似推出线段成比例；若三点定形法不能确定两个相似三角形，则考虑用等量（线段）代换，或用等比代换，然后再用三点定形法确定相似三角形若以上三种方法行不通时，则考虑用等积代换法。参考答案：易求，再证，从而有，即可证3.试一试：如图，在△ABC中，AD、BE分别是BC、AC边上的高，DF⊥AB于F，交AC的延长线于H，交BE于G，求...