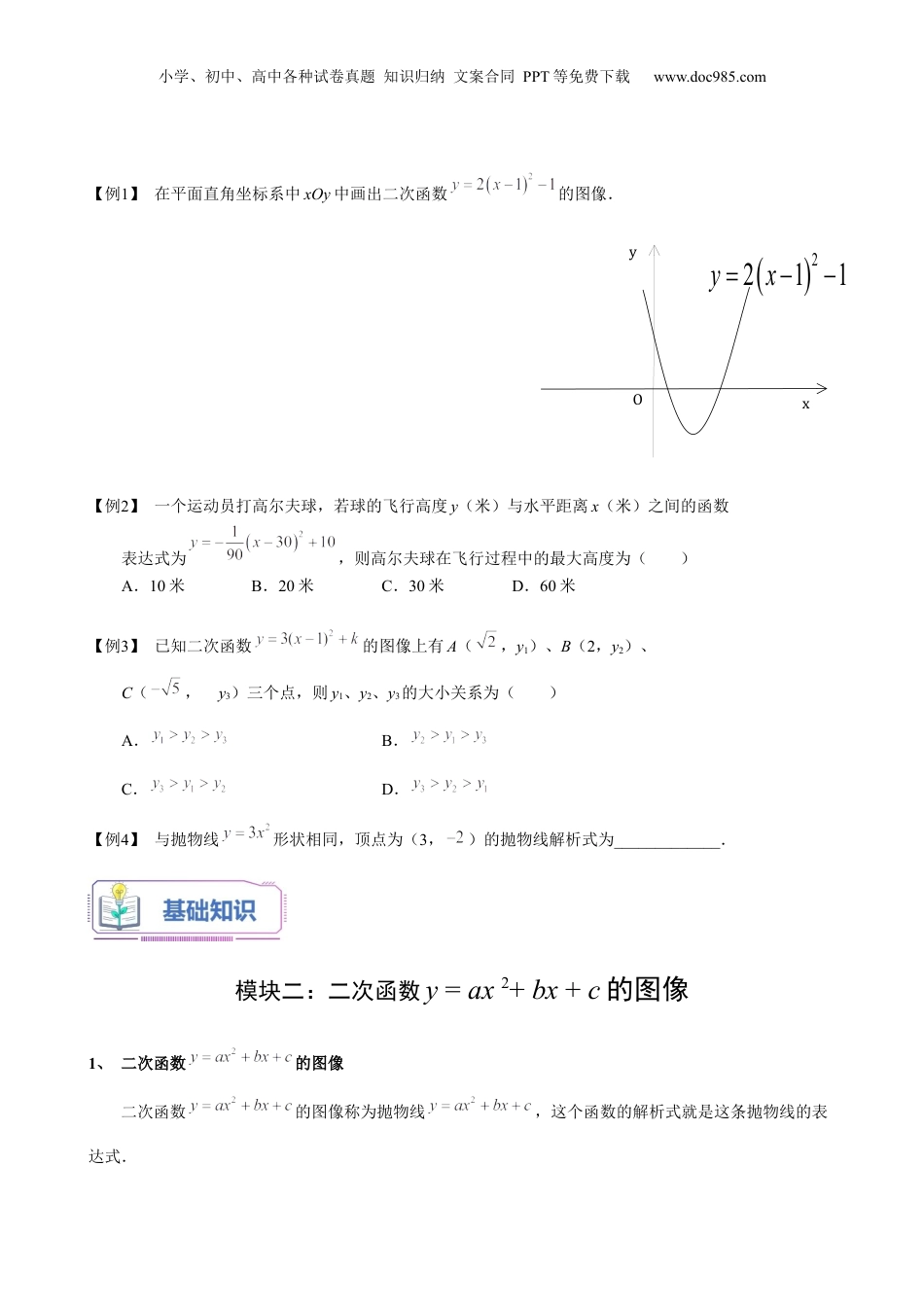
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第17讲二次函数y=ax2+bx+c的图像二次函数的图像的研究,需要利用配方法的方式对进行变形,从而利用的图像特征研究的图像特征,继而掌握a、b、c与二次函数图像的对称轴和顶点的联系.模块一:二次函数y=a(x+m)2+k的图像1、二次函数的图像二次函数(其中a、m、k是常数,且)的图像即抛物线,可以通过将抛物线进行两次平移得到.这两次平移可以是:先向左(时)或向右(时)平移个单位,再向上(时)或向下(时)平移个单位.利用图形平移的性质,可知:抛物线(其中a、m、k是常数,且)的对称轴是经过点(,0)且平行于y轴的直线,即直线x=;抛物线的顶点坐标是(,k).抛物线的开口方向由a所取值的符号决定,当时,开口向上,顶点是抛物线的最低点;当时,开口向下,顶点是抛物线的最高点.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例1】在平面直角坐标系中xOy中画出二次函数的图像.【例2】一个运动员打高尔夫球,若球的飞行高度y(米)与水平距离x(米)之间的函数表达式为,则高尔夫球在飞行过程中的最大高度为()A.10米B.20米C.30米D.60米【例3】已知二次函数的图像上有A(,y1)、B(2,y2)、C(,y3)三个点,则y1、y2、y3的大小关系为()A.B.C.D.【例4】与抛物线形状相同,顶点为(3,)的抛物线解析式为_____________.模块二:二次函数y=ax2+bx+c的图像1、二次函数的图像二次函数的图像称为抛物线,这个函数的解析式就是这条抛物线的表达式.yOx2211yx小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com任意一个二次函数(其中a、b、c是常数,且)都可以运用配方法,把它的解析式化为的形式.对配方得:.由此可知:抛物线(其中a、b、c是常数,且)的对称轴是直线,顶点坐标是(,).当时,抛物线开口向上,顶点是抛物线的最低点,抛物线在对称轴(即直线)左侧的部分是下降的,在对称轴右侧的部分是上升的;当时,抛物线开口向下,顶点是抛物线的最高点,抛物线在对称轴(即直线)左侧的部分是上升的,在对称轴右侧的部分是下降的.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例5】用配方法把下列函数解析式化为的形式.(1);(2).【例6】通过配方,确定抛物线的开口方向、对称轴和顶点坐标,再描点画图.【例7】化成的形式为()A.B.C.D.【例8】在同一直角坐标系中,函数和(m是常数,且)的图像可能是()yOx2218yxA.B.C.D.xyxyxyxy小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【例9】已知一次函数与二次函数的图像都过点A(1,),二次函数的对称轴是直线x=,请求出一次函数和二次函数的解析式.【例10】已知抛物线经过点P(,).(1)求b+c的值;(2)若b=3,求这条抛物线的顶点坐标;(3)若,过点P作直线PAy轴,交y轴与点A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的解析式.一、单选题1.(2023·上海虹口·统考一模)已知二次函数的图像如图所示,那么下列四个结论中,错误的是()A.B.C.D.2.(2023·上海宝山·一模)将抛物线向右平移3个单位长度,平移后抛物线的表达式为()A.B.C.D.3.(2023·上海徐汇·统考一模)二次函数的图像如图所示,点在轴的正半轴上,且,下列选项中正确的是()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA.B.C.D.4.(2023·上海崇明·统考一模)将函数的图像向右平移2个单位,下列结论中正确的是()A.开口方向不变B.顶点不变C.对称轴不变D.与轴的交点不变5.(2023·上海徐汇·统考一模)将抛物线经过下列平移能得到抛物线的是()A.向右个单位,向下个单位B.向左个单位,向下个单位C.向右个单位,向上个单位D.向左个单位,向上个单位6.(2023·上海闵行·统考二模)在平面直角坐标系中,如果把抛物线向下平移3个单位得到一条新抛物线,那么下列关于这两条抛物线的描述中不正确的是()A.开口方向相同;B.对称...