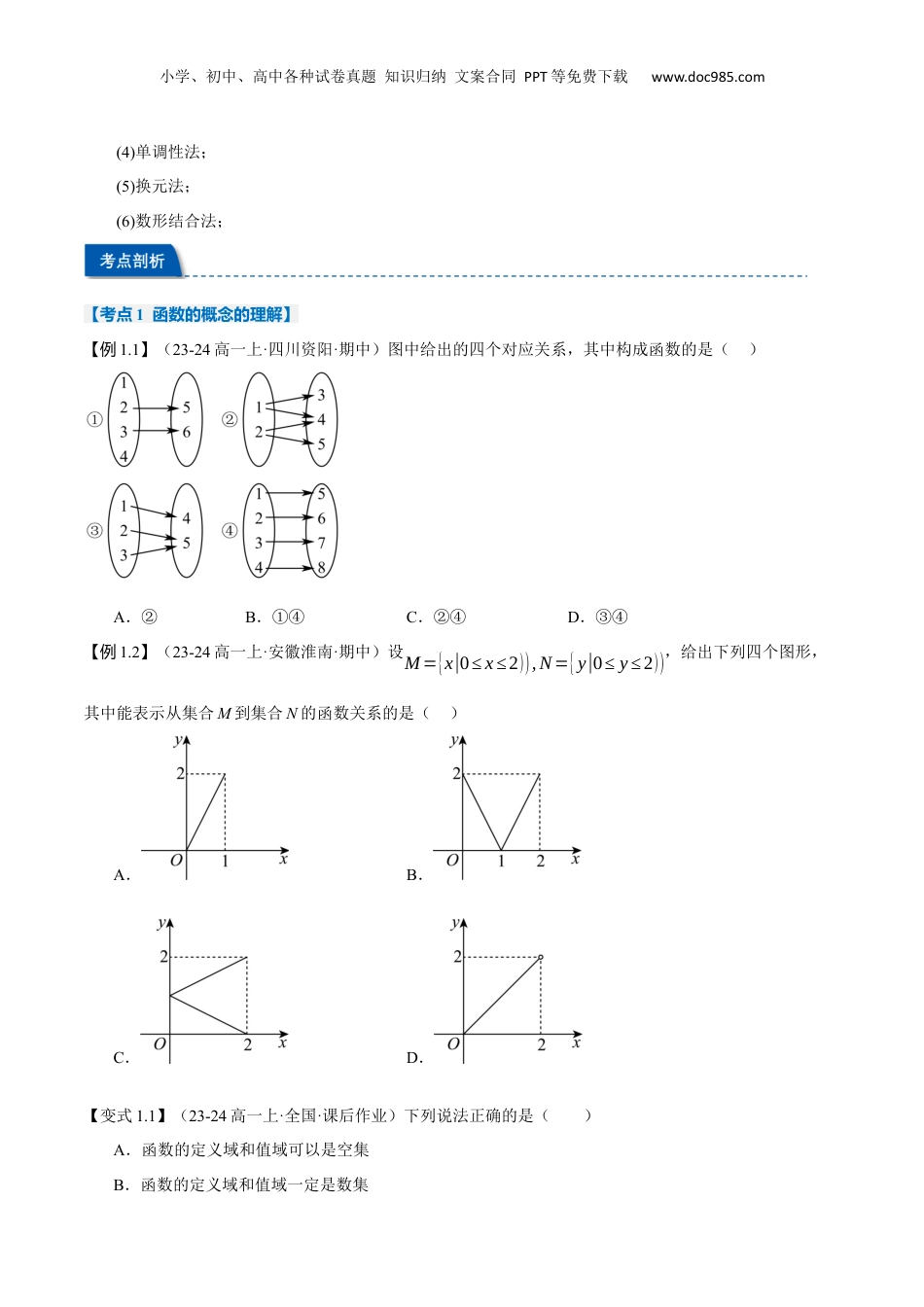
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第09讲函数的概念及其表示【人教A版2019】·模块一函数的概念·模块二函数的相等·模块三函数的表示法·模块四课后作业1．函数的概念(1)一般地，设A，B是非空的实数集，如果对于集合A中的任意一个数x，按照某种确定的对应关系f，在集合B中都有唯一确定的数y和它对应，那么就称f：AB为从集合A到集合B的一个函数(function)，记作y=f(x)，xA.(2)函数的四个特征：①非空性：A，B必须为非空数集，定义域或值域为空集的函数是不存在的.②任意性：即定义域中的每一个元素都有函数值.③单值性：每一个自变量有且仅有唯一的函数值与之对应.④方向性：函数是一个从定义域到值域的对应关系，如果改变这个对应方向，那么新的对应所确定的关系就不一定是函数关系.2．函数的三要素(1)定义域：函数的定义域是自变量的取值范围．(2)值域：与x的值相对应的y值叫做函数值，函数值的集合{f(x)|xA}叫做函数的值域(range).(3)对应关系：对应关系f是函数的核心，它是对自变量x实施“对应操作”的“程序”或者“方法”．3．求给定解析式的函数定义域的方法求给定解析式的函数的定义域，其实质就是以函数解析式中所含式子(运算)有意义为准则，列出不等式或不等式组求解；对于实际问题，定义域应使实际问题有意义.4．求抽象函数定义域的方法(1)若已知函数f(x)的定义域为[a,b]，则复合函数f[g(x)]的定义域可由不等式a≤g(x)≤b求出.(2)若已知函数f[g(x)]的定义域为[a,b]，则f(x)的定义域为g(x)在x[∈a,b]上的值域.5．求函数值域的一般方法(1)分离常数法；(2)配方法；(3)不等式法；函的念数概模一块小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(4)单调性法；(5)换元法；(6)数形结合法；【考点1函数的概念的理解】【例1.1】（23-24高一上·四川资阳·期中）图中给出的四个对应关系，其中构成函数的是（）A．②B．①④C．②④D．③④【例1.2】（23-24高一上·安徽淮南·期中）设M={x|0≤x≤2)),N={y|0≤y≤2))，给出下列四个图形，其中能表示从集合M到集合N的函数关系的是（）A．B．C．D．【变式1.1】（23-24高一上·全国·课后作业）下列说法正确的是（）A．函数的定义域和值域可以是空集B．函数的定义域和值域一定是数集小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．函数值域中每一个数在定义域中一定只有一个数与之对应D．函数的定义域和值域确定后，函数的对应关系也就确定了【变式1.2】（23-24高一上·江苏徐州·期中）已知A={0,1,2)，B={0,1,❑√2,2,4)，下列对应关系不能作为从A到B的函数的是（）A．f:x→y=❑√xB．f:x→y=x2C．f:x→y=1xD．f:x→y=|x)【考点2求函数的定义域】【例2.1】（23-24高一上·北京·期中）函数f(x)=1❑√x−2的定义域为（）A．(0,2)B．(0,2¿C．(2,+∞)D．¿【例2.2】（23-24高一上·甘肃白银·期末）已知函数y=f(x)的定义域是[−1,3)，则y=f(2x−1)的定义域是（）A．[0,2)B．[−1,3)C．[0,4)D．[−52,0)【变式2.1】（23-24高一上·山东·期中）若函数f(x)的定义域为[−1,2)，则函数y=f(x2−1)❑√x+1的定义域为（）A．(−❑√3,2)B．[0,❑√3)C．(−1,2)D．(−1,❑√3)【变式2.2】（23-24高一上·山西·期中）若函数f(x+1)的定义域为(−2,2)，则函数g(x)=f(x)❑√x的定义域为（）A．(0,1)B．(0,3)C．(−1,3)D．(0,+∞)【考点3求函数的值域】【例3.1】（23-24高一上·北京·期中）函数f(x)=x2−2x，x∈[−2,2)的值域是（）A．[−1,0)B．[0,8)C．[1,8)D．[−1,8)【例3.2】（23-24高一上·北京·期中）函数y=1x2+3的值域为（）A．(−∞,13)B．(−∞,13)C．[0,13)D．(0,13)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式3.1】（23-24高一上·山西太原·阶段练习）函数f(x)=❑√−x2−2x+3的值域是（）A．[0,2)B．[0,+∞)C．[2,+∞)D．(0,2)∪(2,+∞)【变式3.2】（23-24高一上·江苏南京·期中）下列函数中，值域是(0,+∞)的是（）A．y=❑√x2−2xB．y=x+2x+1,x∈(0,+∞)C．y=1x2+2x+1,x∈ND．y=1|x−1)【...