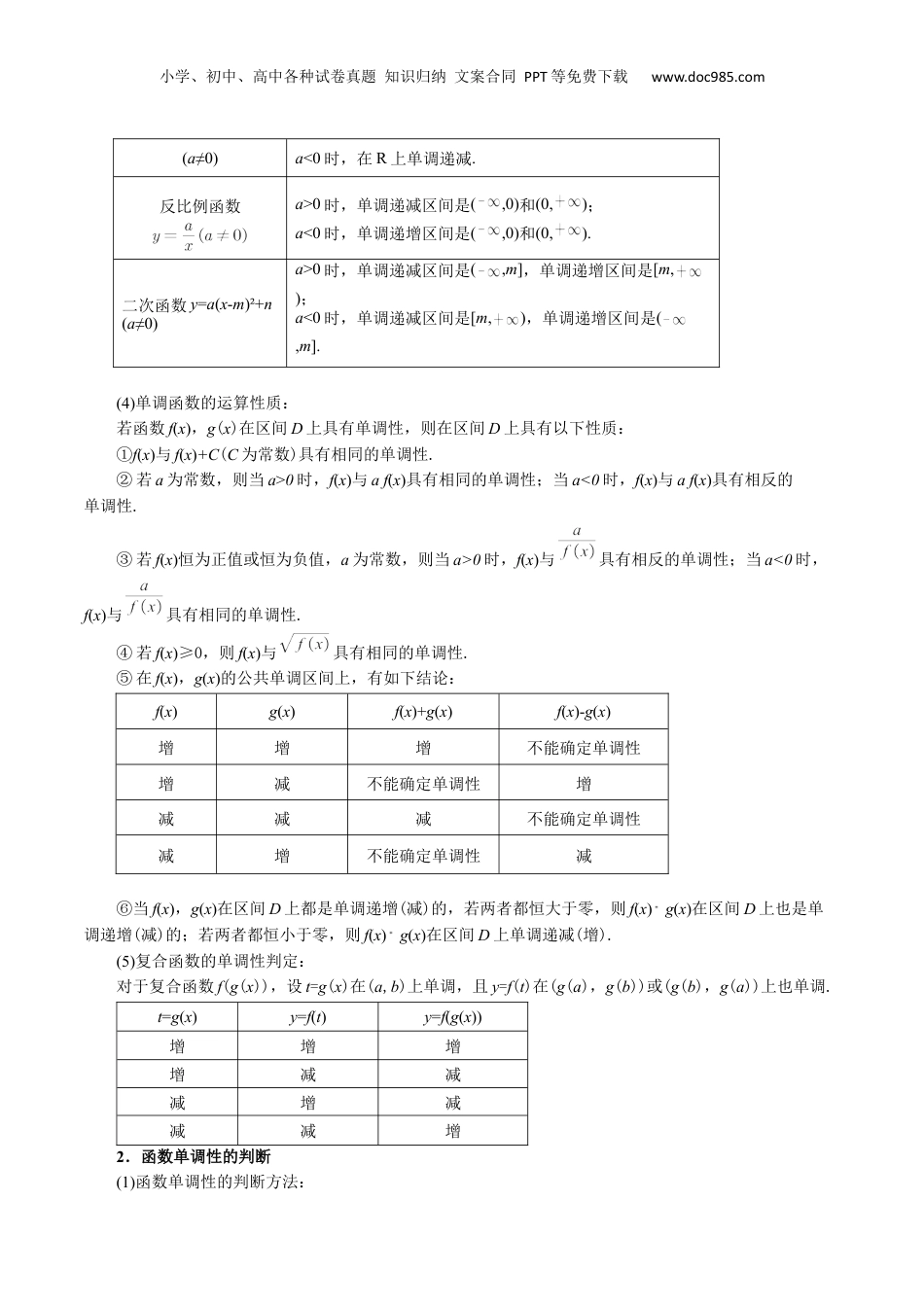
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第10讲函数的单调性和最值【人教A版2019】·模块一函数的单调性·模块二函数的最值·模块三课后作业1．函数的单调性(1)单调递增、单调递减：名称定义图形表示几何意义单调递增一般地，设函数f(x)的定义域为I，区间DI：如果x1,x2∈D，当x1<x2时，都有f(x1)<f(x2)，那么就称函数f(x)在区间D上单调递增.函数f(x)在区间D上的图象从左到右是上升的.单调递减一般地，设函数f(x)的定义域为I，区间DI：如果x1,x2∈D，当x1<x2时，都有f(x1)>f(x2)，那么就称函数f(x)在区间D上单调递减.函数f(x)在区间D上的图象从左到右是下降的.(2)函数的单调性及单调区间：①当函数f(x)在它的定义域上单调递增(减)时,我们就称它是增(减)函数.②如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.(3)常见函数的单调性：函数单调性一次函数y=ax+ba>0时，在R上单调递增；函的性数单调模一块小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(a≠0)a<0时，在R上单调递减.反比例函数a>0时，单调递减区间是(,0)和(0,)；a<0时，单调递增区间是(,0)和(0,).二次函数y=a(x-m)²+n(a≠0)a>0时，单调递减区间是(,m]，单调递增区间是[m,)；a<0时，单调递减区间是[m,)，单调递增区间是(,m].(4)单调函数的运算性质：若函数f(x)，g(x)在区间D上具有单调性，则在区间D上具有以下性质：①f(x)与f(x)+C(C为常数)具有相同的单调性.②若a为常数，则当a>0时，f(x)与af(x)具有相同的单调性；当a<0时，f(x)与af(x)具有相反的单调性.③若f(x)恒为正值或恒为负值，a为常数，则当a>0时，f(x)与具有相反的单调性；当a<0时，f(x)与具有相同的单调性.④若f(x)≥0，则f(x)与具有相同的单调性.⑤在f(x)，g(x)的公共单调区间上，有如下结论：f(x)g(x)f(x)+g(x)f(x)-g(x)增增增不能确定单调性增减不能确定单调性增减减减不能确定单调性减增不能确定单调性减⑥当f(x)，g(x)在区间D上都是单调递增(减)的，若两者都恒大于零，则f(x)g(x)在区间D上也是单调递增(减)的；若两者都恒小于零，则f(x)g(x)在区间D上单调递减(增).(5)复合函数的单调性判定：对于复合函数f(g(x))，设t=g(x)在(a,b)上单调，且y=f(t)在(g(a)，g(b))或(g(b)，g(a))上也单调.t=g(x)y=f(t)y=f(g(x))增增增增减减减增减减减增2．函数单调性的判断(1)函数单调性的判断方法：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com①定义法；②图象法；③利用已知函数的单调性.(2)函数y=f(g(x))的单调性应根据外层函数y=f(t)和内层函数t=g(x)的单调性判断，遵循“同增异减”的原则.【考点1函数单调性的判断及单调区间的求解】【例1.1】（23-24高一上·天津和平·期中）函数y=x+1x的单调递减区间为（）A．(0,1¿B．[−1,1]C．[−1,0)∪(0,1]D．¿，(0,1¿【例1.2】（23-24高一上·广东广州·期中）已知函数f(x)=x+2x−1，则函数f(x)（）A．在(−2,+∞)上单调递增B．在(−2,+∞)上单调递减C．在(1,+∞)上单调递增D．在(1,+∞)上单调递减【变式1.1】（23-24高一上·陕西西安·期中）已知函数f(x)=|x2−5x+6)，则函数f(x)的单调递增区间是（）A．(−∞,52)B．(52,+∞)C．(2,52)和(3,+∞)D．(−∞,2)和(52,3)【变式1.2】（2023高三·全国·专题练习）已知函数y=f(x)的定义域为R，对任意x1，x2且x1≠x2，都有f(x1)−f(x2)x1−x2>−1，则下列说法正确的是（）A．y=f(x)+x是增函数B．y=f(x)+x是减函数C．y=f(x)是增函数D．y=f(x)是减函数【考点2利用函数的单调性求参数】【例2.1】（23-24高一上·安徽马鞍山·期中）函数y=x2+bx+c在(−∞,1)上是单调函数，则b的取值范围是（）A．(−∞,−2¿B．(−∞,−2)C．¿D．(−2,+∞)【例2.2】（23-24高三上·天津河东·阶段练习）设命题P:“函数y=(2a−1)x+a为递减函数”，命题Q:小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com“a<0”，则P是Q的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件...