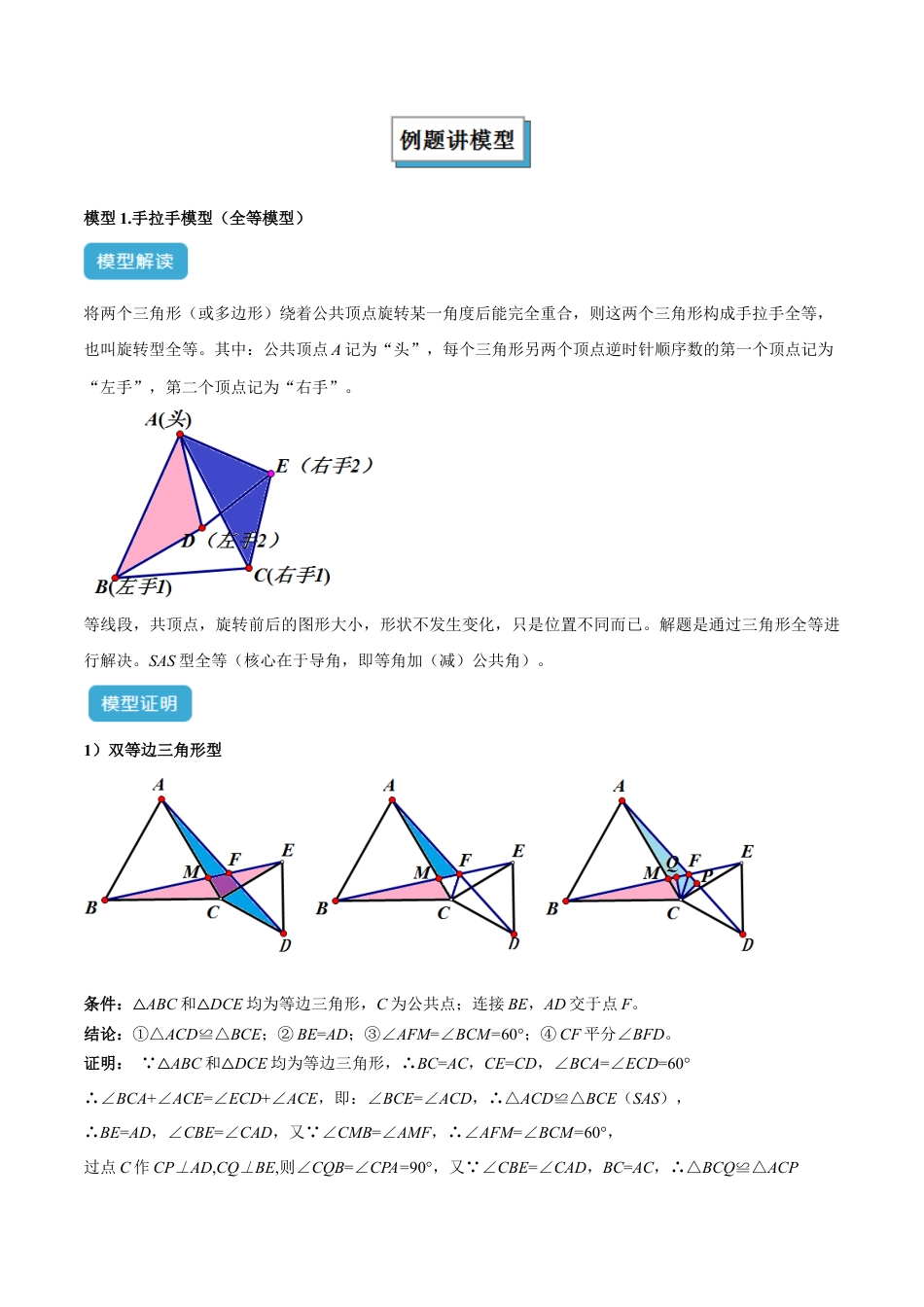
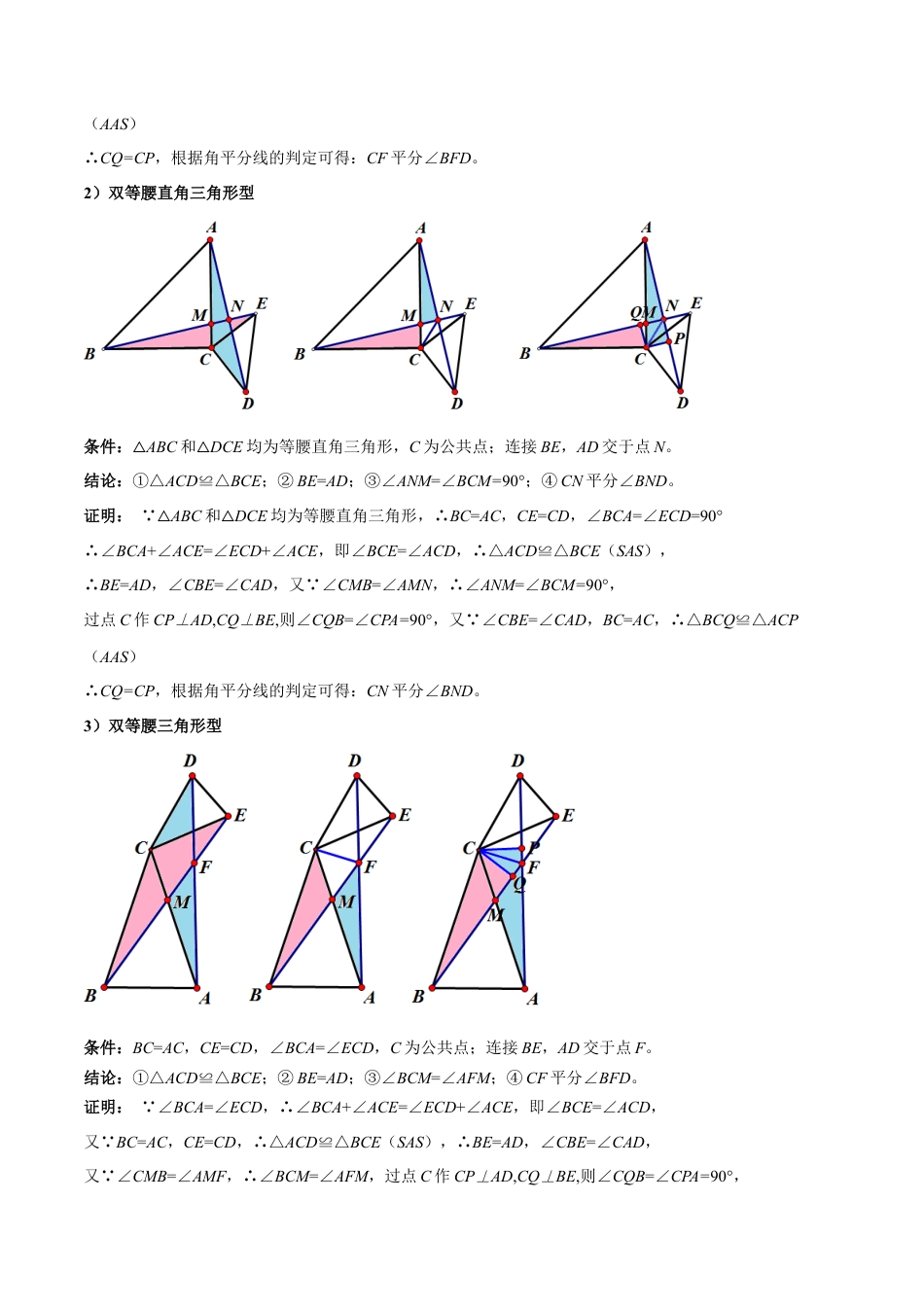
专题20全等与相似模型之手拉手模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。全等三角形、相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了。本专题就手拉手模型进行梳理及对应试题分析,方便掌握。.................................................................................................................................................2模型1.手拉手模型(全等模型)...................................................................................................................2模型2.手拉手模型(相似模型).................................................................................................................12...............................................................................................................................................26大家在掌握几何模型时,多数同学会注重模型结论,而忽视几何模型的证明思路及方法,导致本末倒置。要知道数学题目的考察不是一成不变的,学数学更不能死记硬背,要在理解的基础之上再记忆,这样才能做到对于所学知识的灵活运用,并且更多时候能够启发我们解决问题的关键就是基于已有知识、方法的思路的适当延伸、拓展,所以学生在学习几何模型要能够做到的就是:①认识几何模型并能够从题目中提炼识别几何模型;②记住结论,但更为关键的是记住证明思路及方法;③明白模型中常见的易错点,因为多数题目考察的方面均源自于易错点。当然,以上三点均属于基础要求,因为题目的多变性,若想在几何学习中突出,还需做到的是,在平时的学习过程中通过大题量的训练,深刻认识几何模型,认真理解每一个题型,做到活学活用!模型1.手拉手模型(全等模型)将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。等线段,共顶点,旋转前后的图形大小,形状不发生变化,只是位置不同而已。解题是通过三角形全等进行解决。SAS型全等(核心在于导角,即等角加(减)公共角)。1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。证明: △ABC和△DCE均为等边三角形,∴BC=AC,CE=CD,∠BCA=∠ECD=60°∴∠BCA+∠ACE=∠ECD+∠ACE,即:∠BCE=∠ACD,∴△ACD≌△BCE(SAS),∴BE=AD,∠CBE=∠CAD,又 ∠CMB=∠AMF,∴∠AFM=∠BCM=60°,过点C作CP⊥AD,CQ⊥BE,则∠CQB=∠CPA=90°,又 ∠CBE=∠CAD,BC=AC,∴△BCQ≌△ACP(AAS)∴CQ=CP,根据角平分线的判定可得:CF平分∠BFD。2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BND。证明: △ABC和△DCE均为等腰直角三角形,∴BC=AC,CE=CD,∠BCA=∠ECD=90°∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∴△ACD≌△BCE(SAS),∴BE=AD,∠CBE=∠CAD,又 ∠CMB=∠AMN,∴∠ANM=∠BCM=90°,过点C作CP⊥AD,CQ⊥BE,则∠CQB=∠CPA=90°,又 ∠CBE=∠CAD,BC=AC,∴△BCQ≌△ACP(AAS)∴CQ=CP,根据角平分线的判定可得:CN平分∠BND。3)双等腰三角形型条件:BC=AC,CE=CD,∠BCA=∠ECD,C为公共点;连接BE,AD交于点F。结论:①△ACD≌△BCE;②BE=AD;③∠BCM=∠AFM;④CF平分∠BFD。证明: ∠BCA=∠ECD,∴∠BCA+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,又 BC=AC,CE=CD,∴△ACD≌△BCE(SAS),∴BE=AD,∠CBE=∠CAD,又 ∠CMB=∠AMF,∴∠BCM=∠AFM,过点C作CP⊥AD,CQ⊥BE,则∠CQB=∠CPA=90°,又 ∠CBE=∠CAD,BC=AC,∴△BCQ≌△ACP(AAS)∴CQ=CP,根据角平分线的判定可得:CF平分...