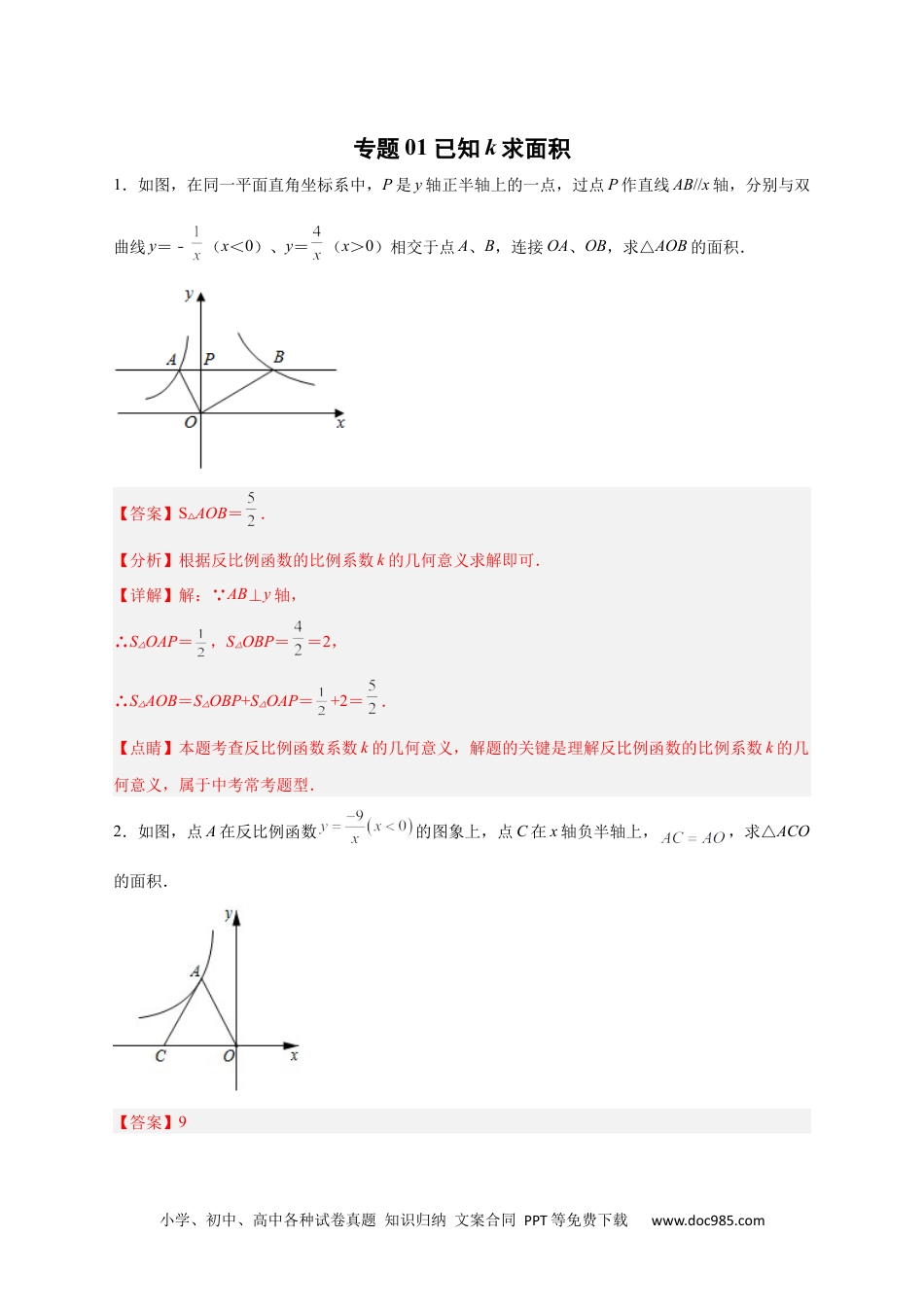
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题01已知k求面积1．如图，在同一平面直角坐标系中，P是y轴正半轴上的一点，过点P作直线AB//x轴，分别与双曲线y＝﹣（x＜0）、y＝（x＞0）相交于点A、B，连接OA、OB，求△AOB的面积．【答案】S△AOB＝．【分析】根据反比例函数的比例系数k的几何意义求解即可．【详解】解： AB⊥y轴，∴S△OAP＝，S△OBP＝＝2，∴S△AOB＝S△OBP+S△OAP＝+2＝．【点睛】本题考查反比例函数系数k的几何意义，解题的关键是理解反比例函数的比例系数k的几何意义，属于中考常考题型．2．如图，点A在反比例函数的图象上，点C在x轴负半轴上，，求△ACO的面积．【答案】9小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】作于点B，设点，根据题意可得，，且，最后根据三角形的面积公式计算求解即可．【详解】解析：如图，过点A作轴，垂足为点B，设点A坐标为，则．又 ．∴，∴，∴．又 点A在反比例函数的图象上，∴代入得，∴．故答案为9．【点睛】本题考查反比例函数k的几何意义、等腰三角形的性质等，熟悉掌握反比例函数的性质、等腰三角形的性质以及三角形的面积公式是本题的解题关键．3．如图，在平面直角坐标系中，四边形OABC为矩形，点B在函数y1＝（x＞0）的图象上，边AB与函数y2＝（x＞0）的图象交于点D．求四边形ODBC的面积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】3【分析】根据反比例函数k的几何意义可知：△AOD的面积为1，矩形ABCO的面积为4，从而可以求出阴影部分ODBC的面积．【详解】解： 点D是函数y2＝（x＞0）图象上的一点，∴△AOD的面积为， 点B在函数y1＝（x＞0）的图象上，四边形ABCO为矩形，∴矩形ABCO的面积为4，∴阴影部分ODBC的面积＝矩形ABCO的面积-△AOD的面积＝4-1＝3，故选：B．【点睛】本题考查反比例函数的几何意义，解题的关键是正确理解的几何意义．4．如图，点M是反比例函数图像上的一个动点，过点M作x轴的平行线交反比例函数图像于点N．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)若点M（，3），求点N的坐标；(2)若点P是x轴上的任意一点，那么△PMN的面积是否发生变化？若不变，求出它的面积是多少？若变化，请说明理由．【答案】(1)(2)不变，5【分析】（1）将y=3代入，求得点N的坐标；（2）连接OM，ON，记MN与y轴的交点为点H，由反比例函数系数k的几何意义求得△MOH和△NOH的面积，得到△MON的面积，由MN∥x轴得到△MON和△MNP的面积相等，从而得到△PMN的面积不变．（1） MNy轴，∴点M、N的y值相等，将y=3代入，得，∴；（2）不变，如图，连接OM，ON，记MN与y轴的交点为点H，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com MNx轴，点M和点N分别在函数和函数图象上，∴，∴，∴S△PMN=5，∴△PMN的面积不变，且△PMN的面积为5．【点睛】本题考查了反比例函数系数k的几何意义，解题的关键是连接MO和NO，得到△MON和△PMN的面积相等．5．如图，在平面直角坐标系xOy中，直线y=ax+b与双曲线交于A（1，3），B（3，m）两点，与x轴交于点C，与y轴交于点D，连接OA，OB．(1)求a，b，k的值；(2)求△OAB的面积；(3)在x轴上是否存在点P，使△PCD的面积等于△OAB的面积的3倍，若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】(1)a=-1，b=4，k=3(2)4(3)存在，P（-2，0）或（10，0）【分析】（1）把A点的坐标代入反例函数解析式即可求出反比例函数解析式，进而得出B的坐标，把A、B的坐标代入一次函数解析式即可求出一次函数解析式；（2）先由直线解析式求得D（0，4），C（4，0），根据△AOB的面积=△BOD的面积-△AOD的面积求得△AOB的面积；（3）根据题意得到PC•OD=12，即=12，即可求得PC的长，从而求得P的坐标．（1）将点A（1，3）代入y=得：3=，解得k=3，故反比例函数的表达式为：y=，将点B（3，m）代入y=得：m=1，故点B（3，1），将点A（1，3），B...