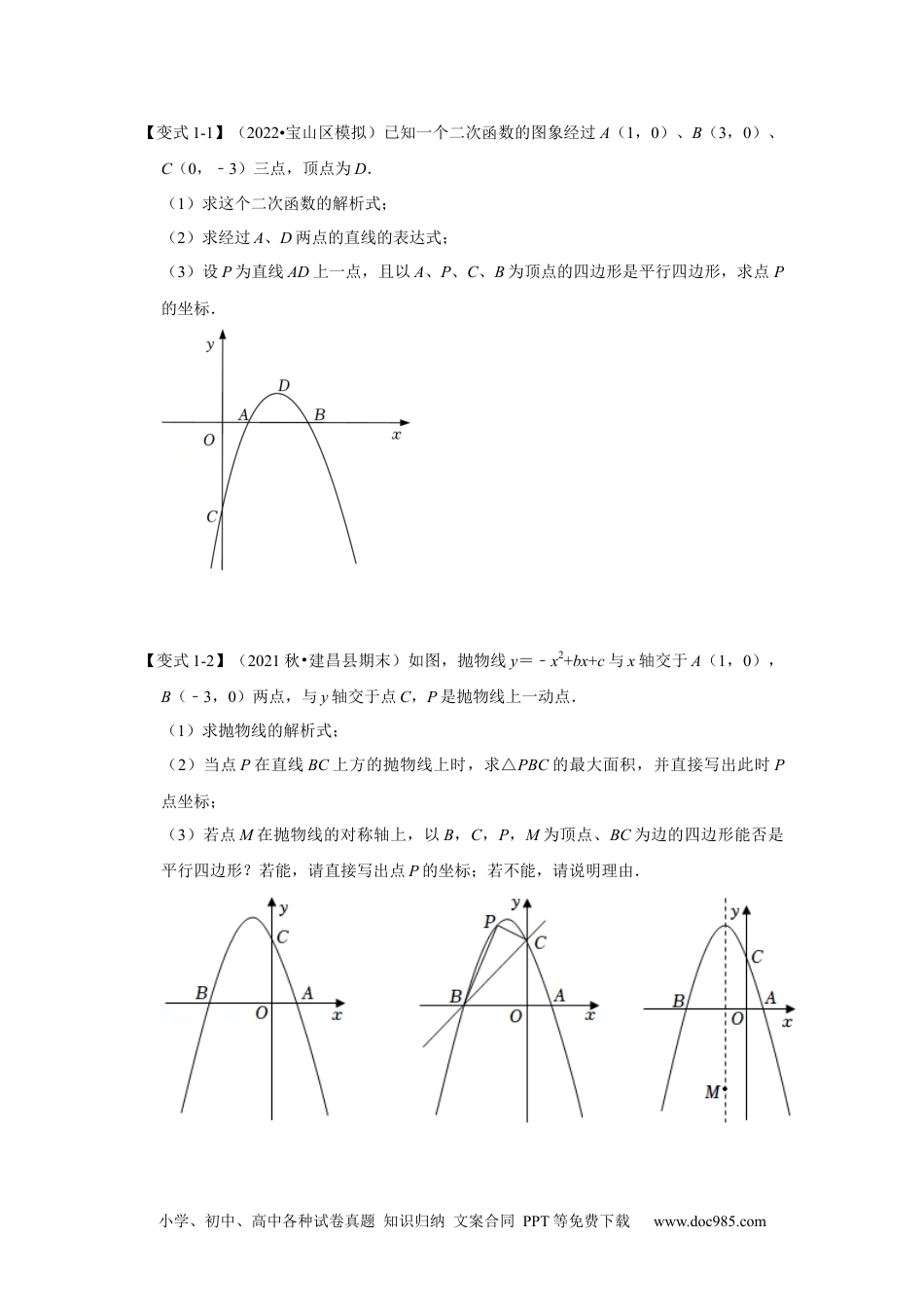
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专项13二次函数与几何综合-特殊平行四边形存在问题知识总结：1.线段中点坐标公式2.平行四边形顶点公式：分类：1.三个定点，一个动点问题已知三个定点的坐标，可设出抛物线上第四个顶点的坐标，运用平行四边形顶点坐标公式列方程（组）求解。这种题型由于三个定点构成的三条线段中哪条为对角线不清楚，往往要以这三条线段分别为对角线分类，分三种情况讨论；2.两个定点、两个动点问题这中题型往往比较特殊，一个动点在抛物线上，另一个动点在x轴（y轴）或对称轴或某一条直线上。设出抛物线上的动点坐标，另一个动点若在x轴上，纵坐标为0，则用平行小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com四边形顶点纵坐标公式；若在y轴上，横坐标为0，则用平行四边形顶点横坐标公式。该动点哪个坐标已知就用与该坐标有关的公式。方法总结：这种题型，关键是合理有序分类：无论式三定一动，还是两定两动，统统把抛物线上的动点作为第四个动点，其余三个作为顶点，分别以这三个定点构成的三条线段为对角线分类，份三种情况讨论，然后运用平行四边形顶点坐标公式转化为方程（组），这种解法，不必画出平行四边形草图，只要合理分类，有序组合，从对角线入手不会漏解，条理清楚，而且适用范围广，其本质用代数的方法解决几何问题，体现的是分类讨论思想、属性结合的思想。【考点1三定一动类型】【典例1】（2022•乐业县二模）如图，抛物线y＝ax2+bx3﹣与x轴交于A（﹣1，0）、B（3，0）两点，直线l与抛物线交于A、C两点，其中点C的横坐标是2．（1）求抛物线的函数表达式；（2）在抛物线的对称轴上找一点P，使得△PBC的周长最小，并求出点P的坐标；（3）在平面直角坐标系中，是否存在一点E，使得以E、A、B、C为顶点的四边形是平行四边形？若存在，求出点E的坐标；若不存在，请说明理由．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式1-1】（2022•宝山区模拟）已知一个二次函数的图象经过A（1，0）、B（3，0）、C（0，﹣3）三点，顶点为D．（1）求这个二次函数的解析式；（2）求经过A、D两点的直线的表达式；（3）设P为直线AD上一点，且以A、P、C、B为顶点的四边形是平行四边形，求点P的坐标．【变式1-2】（2021秋•建昌县期末）如图，抛物线y＝﹣x2+bx+c与x轴交于A（1，0），B（﹣3，0）两点，与y轴交于点C，P是抛物线上一动点．（1）求抛物线的解析式；（2）当点P在直线BC上方的抛物线上时，求△PBC的最大面积，并直接写出此时P点坐标；（3）若点M在抛物线的对称轴上，以B，C，P，M为顶点、BC为边的四边形能否是平行四边形？若能，请直接写出点P的坐标；若不能，请说明理由．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【考点2两定两动类型】【典例2】（2022•牡丹区三模）如图，直线y＝﹣x+4与x轴交于点C，与y轴交于点B，抛物线y＝ax2+x+c经过B，C两点．（1）求抛物线的解析式；（2）E是直线BC上方抛物线上的一动点，当点E到直线BC的距离最大时，求点E的坐标；（3）Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P，Q，B，C为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．【变式2-1】（2022•南京模拟）已知，如图，抛物线与坐标轴相交于点A（﹣1，0），C（0，﹣3）两点，对称轴为直线x＝1，对称轴与x轴交于点D．（1）求抛物线的解析式；（2）点F为二次函数图象上与点C对称的点，点M在抛物线上，点N在抛物线的对称轴上，是否存在以点F，A，M，N为顶点的平行四边形？若存在，直接写出点M的坐标，若不存在，说明理由．【变式2-2】（2022•东莞市校级一模）如图所示，抛物线y＝x2+bx+c交x轴于A、B两点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（点A在点B的左侧），交y轴于点C（0，﹣3），已知AB＝4，对称轴在y轴左侧．（1）求抛物线的表达式；（2）若点N在对称轴上，则抛物线上是否存在点M，使得点A、O、N、M构成平行四边形，若存在，请求出点M的...