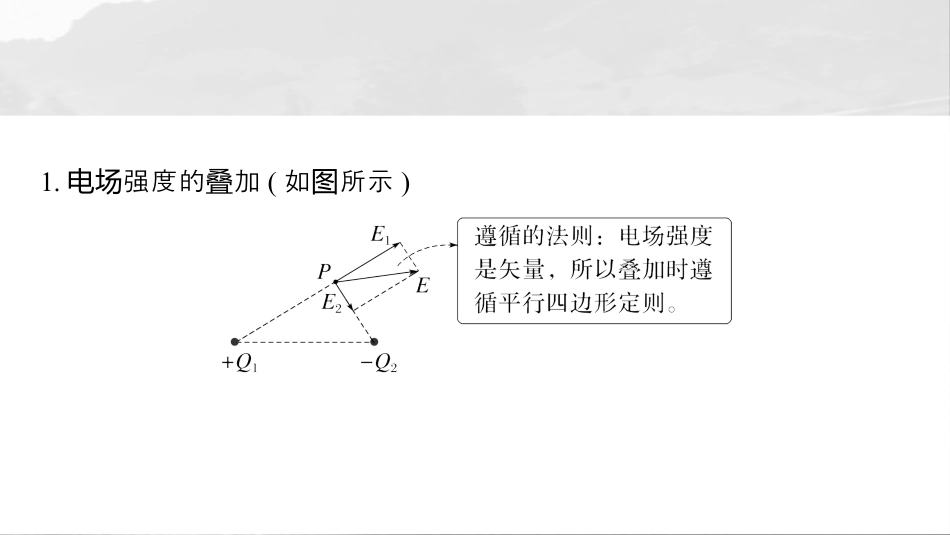
第九章静电场电场强度的叠加目标要求了解常见的电场强度矢量叠加的情形,掌握求电场强度叠加的方法。微点突破41.强度的加电场叠(如所示图)2.强度加常用的其他几方法电场叠种(1)等效法在保效果相同的前提下,的证将复杂电场情景的或熟悉的情景。变换为简单电场例如:一点荷+个电q一无限大薄金与个属板形成的,等效等量点电场为两个异种电荷形成的,如甲、乙所示。电场图(2)法对称利用空上分布的荷形成的具有性的特点,使间对称电电场对称复杂电场的加算化。常的、等在的点生的叠计问题简见圆环圆盘轴对称两产电场具有性。对称(3)法填补有缺口的或板全完整的或板,半球面全将带电圆环圆补为圆环圆将补为球面,而化易、事半功倍。从难为(4)微元法、平面等分成多微元荷,每微元荷可看成点将带电圆环带电许电个电荷,再利用公式和强度加原理求出合强度。电电场叠电场例1(多选)(2024·湖南常德市一中月考)如所示,在直平面以图竖内O点心的上有为圆绝缘圆环A、B、C三点三等分,其中将圆A、B的水平。连线在A、B点各固定一荷量+两个电为Q的点荷,在电C点固定一荷量个电为-2Q的点荷。在电O点有一量个质为M的小球于止,已知带电处静状态圆的半径为R,重力加速度为g,力常量静电为k,下列法正确的是说A.小球正带电B.O点的强度大小电场为kQR2C.小球的荷量带电为MgR23kQD.撤去C点点荷瞬,小球的加速度大小电间为23g√√A、B、C三点的点荷在电O点生的强度产电场方向如所示,由的加原理可知,图电场叠O点的方向直向下,根据平衡件可得,小球电场竖条带,负电A;错误O点的合强度电场为E=2kQR2cos60°+2kQR2=3kQR2,B;错误由平衡件得条Mg=q3kQR2,得q=MgR23kQ,C正确;撤去C点点荷瞬电间E′=kQR2,由牛第二定律有顿Mg-kQqR2=Ma,得a=23g,D正确。例2如所示,均正的金的心图匀带电属圆环圆为O,在垂直于所圆环在平面且心过圆O的上有轴线A、B、C三点,AO=OB=BC=L,当B点放置荷量电为Q的点荷,负电时A点的强度电场为0。若撤去B点的点荷,在负电C点放置荷量电为2Q的正点荷,电时B点的强度大小电场为(k力常量为静电)A.3kQ4L2B.5kQ4L2C.7kQ4L2D.9kQ4L2√A点的强度电场为0,上的荷在则圆环电A点的强度位于电场与B点的荷量电为Q的点荷在负电A点的强度等大反向,即在电场带电圆环A点的强度大小电场为E=kQ2L2=kQ4L2,根据性可知上的荷在对称圆环电B点的强度大小也电场为E=kQ4L2,方向向右;若撤去B点的点荷,在负电C点放置荷量电为2Q的正点荷,根据强度的加原理可知电时电场叠B点的强度大小电场EB=k2QL2-E=7kQ4L2,故选C。例3均的球在球外空生的等效于荷集中于球心匀带电壳间产电场电处生的。如所示,在半球面时产电场图AB上均分布正荷,荷量匀电总电为q,球面半径为R,CD通半球点球心为过顶与O的,在上轴线轴线有M、N点,两OM=ON=2R,已知M点的强度大小电场为E,力常量静电为k,则N点的强度大小电场为A.kq2R2-EB.kq4R2C.kq4R2-ED.kq4R2+E√把心在圆O点的二分之一球完整的壳补为荷量带电为2q的球,在带电壳则M、N两点的强度大小均电场为E0=k·2q2R2=kq2R2。题中左半球在图壳M点生的强度产电场为E,右半球在则壳M点生产的强度电场为E′=E0-E=kq2R2-E,由性知,左半球在对称壳N点生的强度大小也产电场为kq2R2-E,故选A。例4如所示,空中有一荷均分布的正,半图真电匀带电圆环径为r,荷量带电为q,心圆O在x的坐原点,的轴标处圆环边缘A点与x上轴P点的连线与x的角轴夹为37°,力常量静电为k,取sin37°=0.6、cos37°=0.8,整生的在则个圆环产电场P点的强度大小电场为A.27kq125r2B.36kq125r2C.48kq125r2D.64kq125r2√把分圆环为n等份(n足大够),每一的份电荷量为Δq,有则n=qΔq,每小可以看成份点荷,电由点荷的强度公式可知每电电场小生的份产电在场P点的强度大小均电场为E0=kΔqAP2,由几何系关sin37°=rAP,可得E0=9kΔq25r2。在P点,E0在垂直x方向的分量大小轴为Ey,根据性,对称n个Ey的矢量和为0,E0在x轴方向的分量大小为Ex=E0cos37°,n个Ex的矢量和就是生的在圆环产电场P点的强度,即电场E=nEx,解得E=36kq125r2,A、C、D,错误B正确。跟踪训练1.(2...