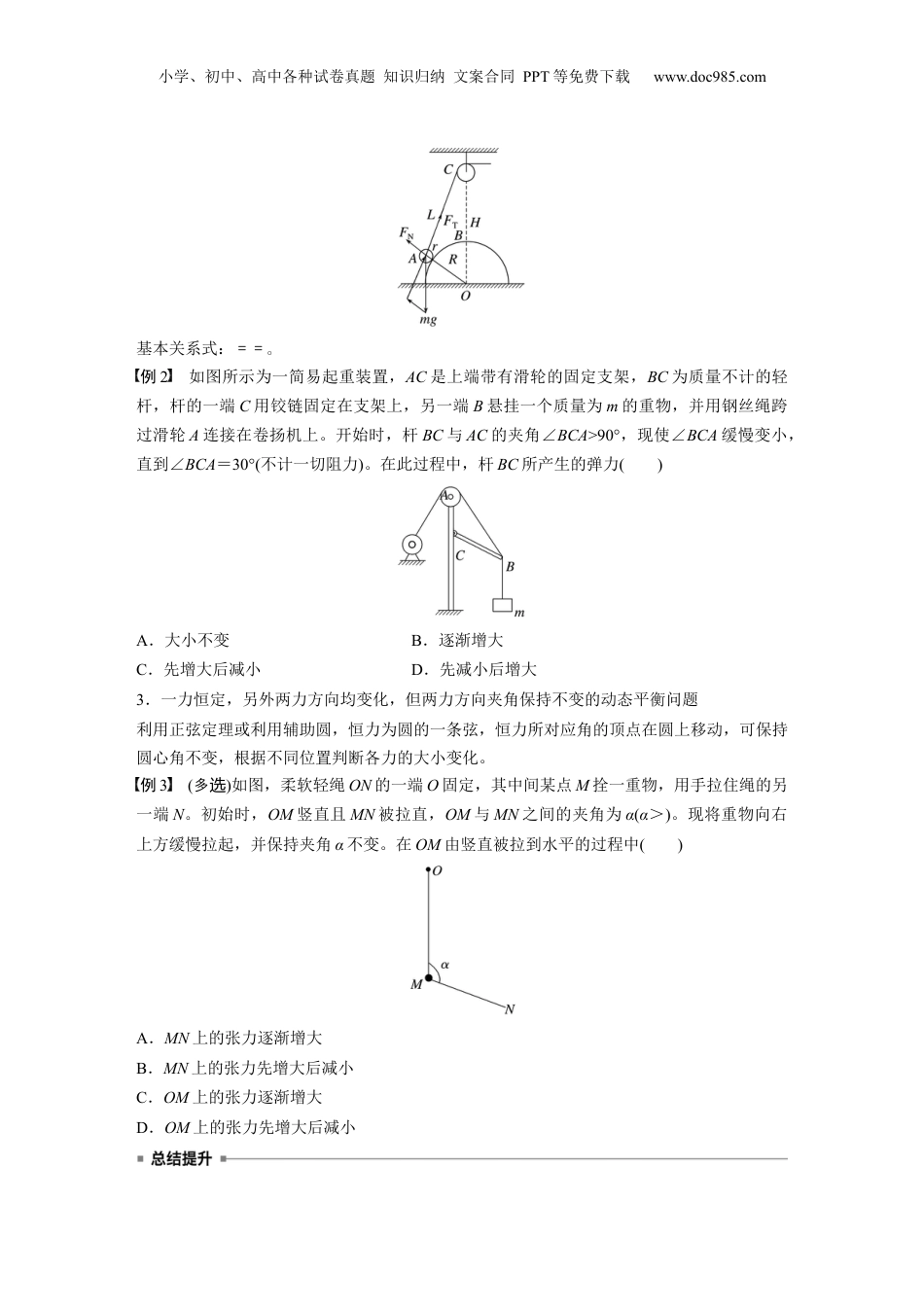
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第4课时专题强化：动态平衡和临界、极值问题目标要求1.学会用图解法、解析法等解决动态平衡问题。2.会分析平衡中的临界与极值问题。考点一动态平衡问题动态平衡是指物体的受力状态缓慢发生变化，但在变化过程中，每一个状态均可视为平衡状态。常用方法：图解法、解析法、相似三角形法、辅助圆法、正弦定理法。1．“一力恒定，另一力方向不变”的动态平衡问题(1)一个力恒定，另一个力始终与恒定的力垂直，三力可构成直角三角形，可作不同状态下的直角三角形，分析力的大小变化，如图甲所示。(2)一力恒定，另一力与恒定的力不垂直但方向不变，作出不同状态下的矢量三角形，确定力大小的变化，在变化过程中恒力之外的两力垂直时，会有极值出现，如图乙所示。例1(多选)如图所示，在倾角为α的斜面上，放一质量为m的小球，小球和斜面及挡板间均无摩擦，当挡板绕O点逆时针缓慢地转向水平位置的过程中()A．斜面对球的支持力逐渐增大B．斜面对球的支持力逐渐减小C．挡板对小球的弹力先减小后增大D．挡板对小球的弹力先增大后减小2．“一力恒定，另两力方向均变化”的动态平衡问题一力恒定(如重力)，其他二力的方向均变化，但二力分别与绳子、两物体重心连线方向等平行，即三力构成的矢量三角形与绳长、半径、高度等实际几何三角形相似，则对应边比值相等。基本矢量图，如图所示小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com基本关系式：＝＝。例2如图所示为一简易起重装置，AC是上端带有滑轮的固定支架，BC为质量不计的轻杆，杆的一端C用铰链固定在支架上，另一端B悬挂一个质量为m的重物，并用钢丝绳跨过滑轮A连接在卷扬机上。开始时，杆BC与AC的夹角∠BCA>90°，现使∠BCA缓慢变小，直到∠BCA＝30°(不计一切阻力)。在此过程中，杆BC所产生的弹力()A．大小不变B．逐渐增大C．先增大后减小D．先减小后增大3．一力恒定，另外两力方向均变化，但两力方向夹角保持不变的动态平衡问题利用正弦定理或利用辅助圆，恒力为圆的一条弦，恒力所对应角的顶点在圆上移动，可保持圆心角不变，根据不同位置判断各力的大小变化。例3(多选)如图，柔软轻绳ON的一端O固定，其中间某点M拴一重物，用手拉住绳的另一端N。初始时，OM竖直且MN被拉直，OM与MN之间的夹角为α(α＞)。现将重物向右上方缓慢拉起，并保持夹角α不变。在OM由竖直被拉到水平的过程中()A．MN上的张力逐渐增大B．MN上的张力先增大后减小C．OM上的张力逐渐增大D．OM上的张力先增大后减小小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com分析动态平衡问题的流程受力分析―――――――→不同下的受力平衡造矢量三角形画状态图构―――――――→考点二平衡中的临界、极值问题1．临界问题当某物理量变化时，会引起其他几个物理量的变化，从而使物体所处的平衡状态“恰好出现”或“恰好不出现”，在问题的描述中常用“刚好”“恰能”“恰好”等。临界问题常见的种类：(1)由静止到运动，摩擦力达到最大静摩擦力。(2)绳子恰好绷紧，拉力F＝0。(3)刚好离开接触面，支持力FN＝0。2．极值问题平衡中的极值问题，一般指在力的变化过程中的最大值和最小值问题。3．解题方法(1)极限法：首先要正确地进行受力分析和变化过程分析，找出平衡的临界点和极值点；临界条件必须在变化中去寻找，不能停留在一个状态来研究临界问题，而要把某个物理量推向极端，即极大和极小。(2)数学分析法：通过对问题的分析，根据物体的平衡条件写出物理量之间的函数关系(或画出函数图像)，用数学方法求极值(如求二次函数极值、公式极值、三角函数极值)。(3)物理分析方法：根据物体的平衡条件，作出力的矢量图，通过对物理过程的分析，利用平行四边形定则进行动态分析，确定最大值与最小值。例4(2023·河南洛市期末阳)如图所示，一光滑球体放在支架与竖直墙壁之间，支架的倾角θ＝60°，光滑球体的质量为m，支架的质量为2m，已知最大静摩擦力等于滑动摩擦力，整个装置保持静止，则支架和地面间的动摩擦因数至少为()A.B.C.D.例5如图所示，质量m...