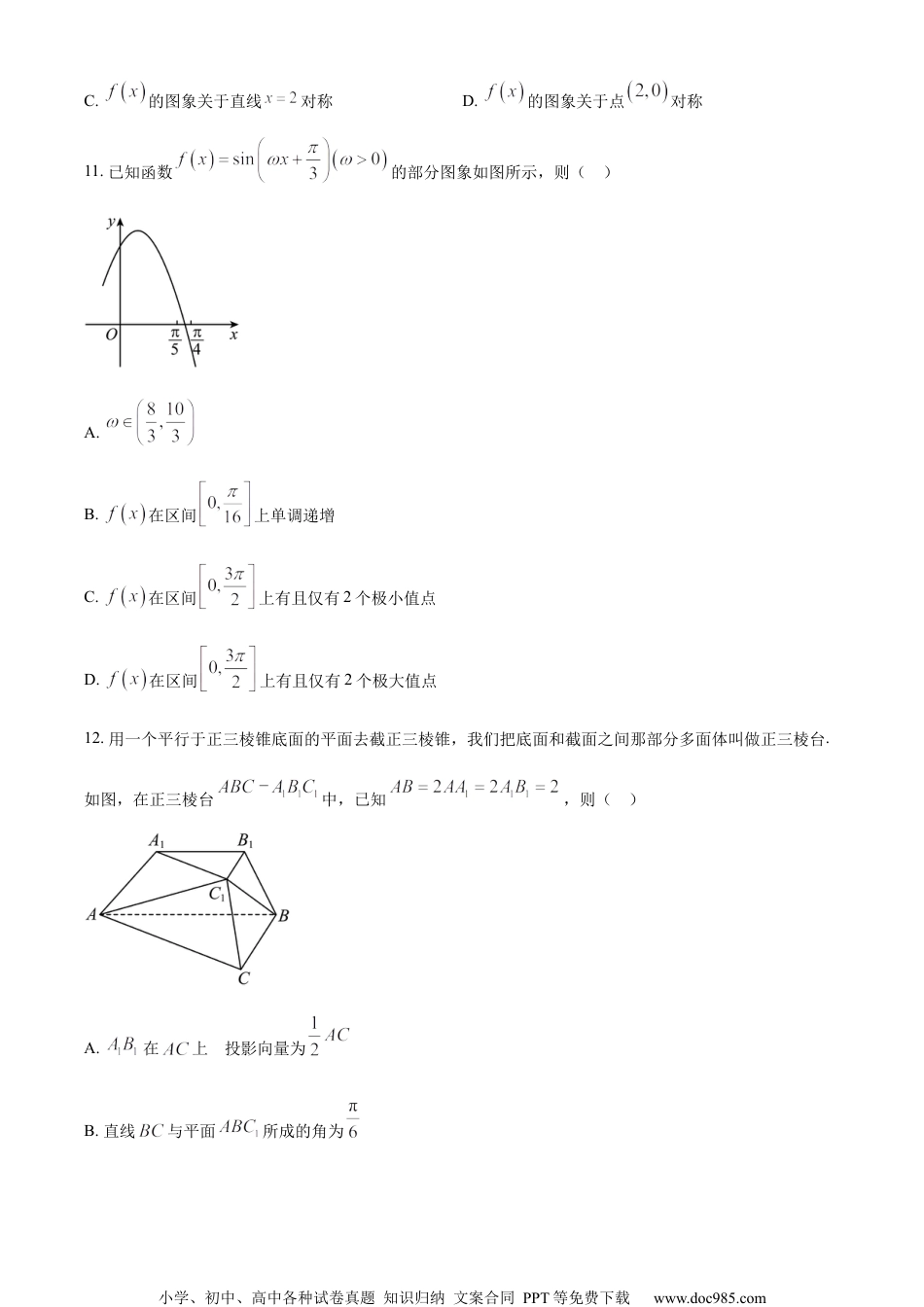
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2023届江苏省无锡市等4地高三数学试题（三模）一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合，集合，则图中阴影部分表示的集合为（）A.B.C.D.2.已知为虚数单位，复数满足，则的虚部为（）A.B.C.1D.23.已知，是空间中两条不同的直线，，，是空间中三个不同的平面，则下列命题中错误的是（）A.若，，则B.若，，则C.若，，，则D.若，，，则4.“青年兴则国家兴，青年强则国家强”，作为当代青少年，我们要努力奋斗，不断进步.假设我们每天进步1%，则一年后的水平是原来的倍，这说明每天多百分之一的努力，一年后的水平将成倍增长.如果将我们每天的“进步”率从目前的10%提高到20%，那么大约经过（）天后，我们的水平是原来应达水平的1500倍.（参考数据：，，）A.82B.84C.86D.88小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5.已知，，若，则（）A.B.C.D.6.已知，为两个随机事件，，，，，则（）A.0.1B.C.0.33D.7.已知点在双曲线上，到两渐近线的距离为，，若恒成立，则的离心率的最大值为（）A.B.C.2D.8.设，，，则（）A.B.C.D.二、选择题：本题共4小题，每小题5分，共20分，在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.在中，若，则（）A.B.C.D.10.已知函数的定义域为，为奇函数，为偶函数，则（）A.的图象关于直线对称B.的图象关于点对称小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC.的图象关于直线对称D.的图象关于点对称11.已知函数的部分图象如图所示，则（）A.B.在区间上单调递增C.在区间上有且仅有2个极小值点D.在区间上有且仅有2个极大值点12.用一个平行于正三棱锥底面的平面去截正三棱锥，我们把底面和截面之间那部分多面体叫做正三棱台.如图，在正三棱台中，已知，则（）A.在上的投影向量为B.直线与平面所成的角为小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC.点到平面的距离为D.正三棱台存在内切球，且内切球半径为三、填空题：本题共4小题，每小题5分，共20分.13.已知函数满足：①为偶函数；②的图象过点；③对任意的非零实数，，.请写出一个满足上述条件的函数______.14.已约是一组平面向量，记，若，则满足的的值为______.15.已如，是抛物线上的动点（异于顶点），过作圆的切线，切点为，则的最小值为______.16.定义：若函数图象上存在相异的两点，满足曲线在和处的切线重合，则称是“重切函数”，，为曲线的“双重切点”，直线为曲线的“双重切线”.由上述定义可知曲线的“双重切线”的方程为______.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.记为数列的前项和，已知，.（1）求的通项公式；（2）记，数列的前项和为，求除以3的余数.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com18.已知的内角，，所对的边分别是，，，且______.在①；②；③这三个条件中任选一个，补充在上面横线上，并加以解答.（1）求；（2）若，，点为的中点，点满足，且，相交于点，求.（注：如果选择多个条件分别解答，按第一个解答计分）19.如图，已知在平面四边形中，，，，现将沿翻折到的位置，使得.（1）求证：平面平面；（2）点在线段上，当二面角的大小为时，确定点的位置.20.为调查学生数学建模能力的总体水平，某地区组织10000名学生（其中男生4000名，女生6000名）参加数学建模能力竞赛活动.（1）若将成绩在的学生定义为“有潜力的学生”，经统计，男生中有潜力的学生有2500名，女生中有潜力的学生有3500名，完成下面的列联表，并判断是否有99.9%的把握认为学生是否有潜力与性别有关?是否有潜力性别合计男生女生小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com有潜力没有潜力合计（2）经统计，男生成绩的均值为80，方差为49，女生成绩的均值为75，方差为64.（ⅰ）求全体参赛学生成绩的均值及方差；（ⅱ）若...