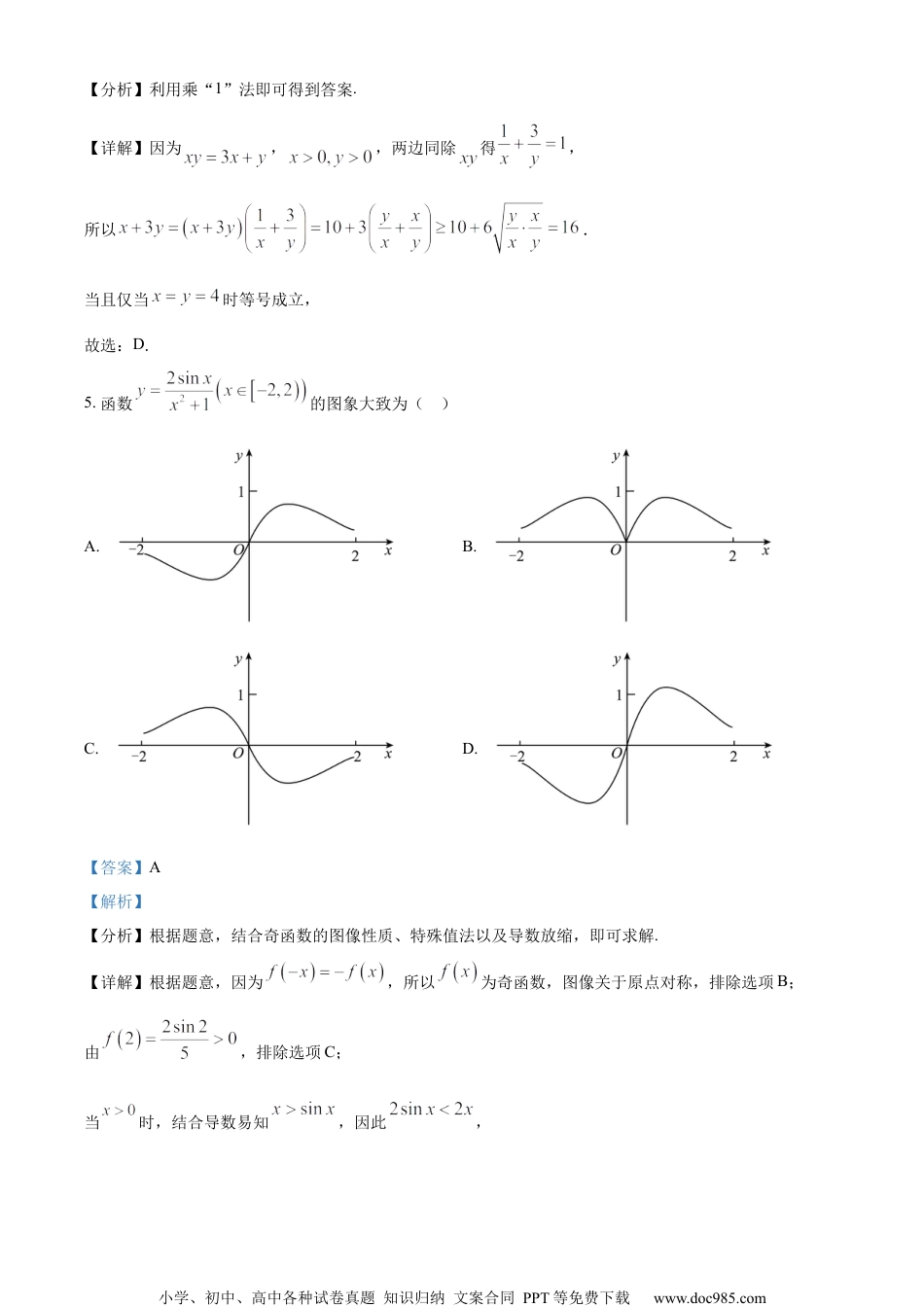
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com决胜新高考—2024届高三年级大联考数学试卷本试卷共6页，22小题，满分150分．考试时间120分钟．注意事项：1．答卷前，考生务必将自己的姓名考生号考场号和座位号填写在答题卡上．将条形码横贴､､在答题卡“条形码粘贴处”．2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案．答案不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液．不按以上要求作答无效．4．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回．一选择题：本题共､8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知复数z满足，则（）A.B.C.D.【答案】B【解析】【分析】根据题意，得到，结合复数模的性质，即可求解.【详解】由复数z满足，可得，则．故选：B.2.设＝{1，2，3，4，5}，若＝{2}，，，则下列结论正确的是A.且B.且小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC.且D.且【答案】B【解析】【分析】根据题意画出韦恩图，确定出A与B,即可作出判断.【详解】因为＝{1，2，3，4，5}，若＝{2}，，，所以画出韦恩图：，，则且，故选B.【点睛】本题主要考查了集合的交、并、补集的混合运算，集合的韦恩图，属于中档题.3.已知不共线的两个非零向量，则“与所成角为锐角”是“”的（）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】【分析】根据向量的运算结合充分、必要条件分析判断.【详解】因为不共线，可知与不共线，则与所成角为锐角等价于，即，即，所以“与所成角为锐角”是“”的充分必要条件.故选：C.4.若满足，则的最小值为（）A.B.C.12D.16【答案】D【解析】小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】利用乘“1”法即可得到答案.【详解】因为，，两边同除得，所以．当且仅当时等号成立，故选：D.5.函数的图象大致为（）A.B.C.D.【答案】A【解析】【分析】根据题意，结合奇函数的图像性质、特殊值法以及导数放缩，即可求解.【详解】根据题意，因为，所以为奇函数，图像关于原点对称，排除选项B；由，排除选项C；当时，结合导数易知，因此，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故当时，，当且仅当时，等号成立，因此当时，，排除选项D.故选：A.6.已知函数在上单调递减，则ω的取值范围是（）A.B.C.D.【答案】B【解析】【分析】令，得，进而根据已知推得.根据式子的意义及的范围，推得，即可得出答案.【详解】令，得.由可得，.因为，所以，所以；又，所以，所以.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，，此时有.故选：B.7.已知，则（）A.B.C.D.【答案】B【解析】【分析】已知等式利用两角和的正弦公式和辅助角公式化简得，再利用诱导公式求的值.【详解】由，得，所以故选：B8.已知，，，则（）A.B.C.D.【答案】A【解析】【分析】构造函数，由易得；构造函数，由导数与函数的单调性求得的单调性，从而证得；由此可得.【详解】令，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以时，，因为，即，所以，故，即，令，则，显然在单调递增，令，得，故在上单调递增，因为，故，则，故在上单调递增，则，即，即，故，综上：.故选：A.二多选题：本题共､4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.已知，则（）A.B.C.D.【答案】BD【解析】【分析】根据对数函数的单调性及取特殊值，，即可判断A；根据幂函数的单调性即可判断B；取特殊值，即可判断C；根据指数函数的单调性即可判断D．【详解】对于A，由函数在上单调递增，小学、初中、高中各种试卷真题知...